سيجمابلوت تركيب المنحنى والانحدار
سيجمابلوت تركيب المنحنى والانحدار
تركيب المنحنى هو العثور على منحنى يطابق سلسلة من نقاط البيانات وربما قيود أخرى.
غالبًا ما يستخدمه العلماء والمهندسون لتصور ورسم المنحنى الذي يصف بشكل أفضل شكل وسلوك بياناتهم.
- تجد إجراءات الانحدار ارتباطًا بين المتغيرات المستقلة والتابعة التي تنتج، عند رسمها بيانيًا، خطًا مستقيمًا أو مستوى أو منحنى.
- المتغيرات المستقلة هي المتغيرات المعروفة أو المتنبئة. غالبًا ما تكون هذه هي قيم المحور X الخاصة بك. تسمى المتغيرات التابعة أيضًا بمتغيرات الاستجابة وهي غالبًا قيم المحور ص.
- يبحث الانحدار عن المعادلة التي تصف البيانات الفعلية أو تناسبها بشكل وثيق، وذلك باستخدام قيم متغير مستقل واحد أو أكثر للتنبؤ بقيمة المتغير التابع. ويمكن بعد ذلك رسم المعادلة الناتجة على البيانات الأصلية لإنتاج منحنى يناسب البيانات.
تركيب منحنى ديناميكي
يعد تركيب المنحنى غير الخطي عملية تكرارية قد تتقارب لإيجاد أفضل حل ممكن. يبدأ الأمر بتخمين المعلمات، والتحقق لمعرفة مدى توافق المعادلة، ويستمر في تقديم تخمينات أفضل حتى لا تنخفض الاختلافات بين مجموع المربعات المتبقية بشكل ملحوظ. بالنسبة لمشاكل تركيب المنحنى المعقدة، استخدم معالج التناسب الديناميكي الخاص بـ SigmaPlot للعثور على الحل الأفضل.
- يقوم معالج التناسب الديناميكي بأتمتة البحث عن قيم المعلمات الأولية التي تؤدي إلى التقارب مع أفضل حل ممكن.
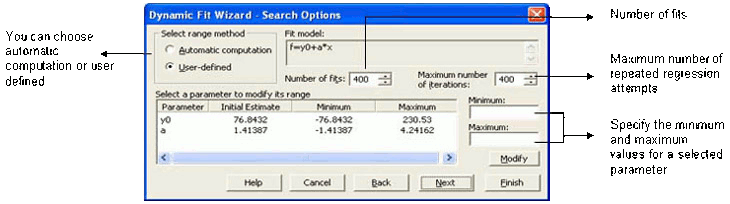
- مثل معالج الانحدار، يعد معالج التناسب الديناميكي بمثابة دليل خطوة بخطوة خلال إجراءات ملاءمة المنحنى، ولكن مع لوحة إضافية تقوم فيها بتعيين خيارات البحث (في الشكل أدناه).
يرجى ملاحظة أن معالج التناسب الديناميكي مفيد بشكل خاص في حل مشكلات ملاءمة المنحنى الأكثر صعوبة مع ثلاثة معلمات أو أكثر وربما قدر كبير من التباين في نقاط البيانات. بالنسبة للانحدارات الخطية أو المشكلات الأقل صعوبة، مثل الملاءمة الأسية البسيطة لمعلمتين، فإن معالج التناسب الديناميكي مبالغ فيه ويجب عليك استخدام معالج الانحدار.
استخدم معالج التناسب الديناميكي من أجل:
- إزالة ضوضاء القياس
- قم بملء نقاط البيانات المفقودة، كما هو الحال عندما يكون قياس واحد أو أكثر مفقودًا أو تم تسجيله بشكل غير صحيح
- الاستيفاء، وهو تقدير البيانات بين نقاط البيانات، كما لو كان الوقت بين القياسات ليس صغيرًا بدرجة كافية
- الاستقراء، وهو تقدير البيانات خارج نقاط البيانات، مثل البحث عن قيم البيانات قبل القياس أو بعده
- التمييز بين البيانات الرقمية، مثل العثور على مشتق نقاط البيانات عن طريق نمذجة البيانات المنفصلة باستخدام كثيرة الحدود والتمييز بين المعادلة متعددة الحدود الناتجة
- دمج البيانات الرقمية، مثل العثور على المنطقة الواقعة أسفل المنحنى عندما يكون لديك فقط النقاط المنفصلة للمنحنى
- احصل على مسار جسم ما بناءً على قياسات منفصلة لسرعته، وهي المشتقة الأولى، أو التسارع، وهو المشتقة الثانية
روابط لمزيد من المعلومات التقنية والأمثلة حول مدى سهولة تركيب المنحنى باستخدام SigmaPlot