SigmaPlot Kurvenanpassung und Regression
SigmaPlot Kurvenanpassung und Regression
Bei der Kurvenanpassung geht es darum, eine Kurve zu finden, die einer Reihe von Datenpunkten und möglicherweise anderen Einschränkungen entspricht.
Sie wird am häufigsten von Wissenschaftlern und Ingenieuren verwendet, um die Kurve zu visualisieren und aufzuzeichnen, die die Form und das Verhalten ihrer Daten am besten beschreibt.
- Bei Regressionsverfahren wird ein Zusammenhang zwischen unabhängigen und abhängigen Variablen gefunden, der bei einer grafischen Darstellung eine gerade Linie, Ebene oder Kurve ergibt.
- Die unabhängigen Variablen sind die bekannten oder prädiktiven Variablen. Dies sind meist die Werte der X-Achse. Die abhängigen Variablen werden auch als Antwortvariablen bezeichnet und sind meist die Werte auf der Y-Achse.
- Bei der Regression wird die Gleichung gefunden, die die tatsächlichen Daten am besten beschreibt oder zu ihnen passt, indem die Werte einer oder mehrerer unabhängiger Variablen zur Vorhersage des Wertes einer abhängigen Variablen verwendet werden. Die sich daraus ergebende Gleichung kann dann über die ursprünglichen Daten aufgetragen werden, um eine Kurve zu erstellen, die zu den Daten passt.
Dynamische Kurvenanpassung
Die nichtlineare Kurvenanpassung ist ein iterativer Prozess, der zu einer bestmöglichen Lösung konvergieren kann. Es beginnt mit einer Schätzung der Parameter, prüft, wie gut die Gleichung passt, und fährt fort, bessere Schätzungen vorzunehmen, bis die Unterschiede zwischen den Restquadratsummen nicht mehr signifikant abnehmen. Für komplizierte Kurvenanpassungsprobleme verwenden Sie den Dynamic Fit Wizard von SigmaPlot, um die beste Lösung zu finden.
- Der Dynamic Fit Wizard automatisiert die Suche nach anfänglichen Parameterwerten, die zur Konvergenz mit der bestmöglichen Lösung führen.
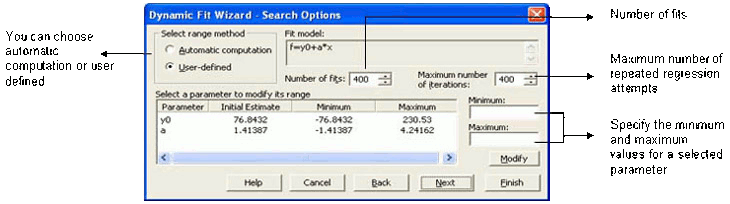
- Wie der Regressionsassistent ist auch der Assistent für die dynamische Anpassung eine schrittweise Anleitung durch die Verfahren der Kurvenanpassung, jedoch mit einem zusätzlichen Panel, in dem Sie die Suchoptionen festlegen (siehe Abbildung unten).
Bitte beachten Sie, dass der Assistent zur dynamischen Anpassung vor allem bei schwierigeren Kurvenanpassungsproblemen mit drei oder mehr Parametern und möglicherweise einer großen Variabilität in den Datenpunkten nützlich ist. Für lineare Regressionen oder weniger schwierige Probleme, wie z. B. einfache exponentielle Zwei-Parameter-Anpassungen, ist der Dynamische Anpassungsassistent überflüssig und Sie sollten den Regressionsassistenten verwenden.
Verwenden Sie den Assistenten für die dynamische Anpassung:
- Messrauschen entfernen
- Füllen Sie fehlende Datenpunkte auf, z. B. wenn eine oder mehrere Messungen fehlen oder nicht ordnungsgemäß aufgezeichnet wurden.
- Interpolieren, d. h. Schätzen von Daten zwischen Datenpunkten, z. B. wenn die Zeit zwischen den Messungen nicht klein genug ist
- Extrapolieren, d. h. die Schätzung von Daten über Datenpunkte hinaus, z. B. die Suche nach Datenwerten vor oder nach einer Messung
- Differenzierung digitaler Daten, z. B. Ermittlung der Ableitung der Datenpunkte durch Modellierung der diskreten Daten mit einem Polynom und Differenzierung der resultierenden Polynomgleichung
- Integration digitaler Daten, z. B. Ermittlung der Fläche unter einer Kurve, wenn Sie nur die einzelnen Punkte der Kurve haben
- Ermittlung der Flugbahn eines Objekts auf der Grundlage diskreter Messungen seiner Geschwindigkeit (erste Ableitung) oder seiner Beschleunigung (zweite Ableitung)
Links zu weiteren technischen Informationen und Beispielen, wie die Kurvenanpassung mit SigmaPlot einfach ist
