シグマ・プロット 曲線フィットと回帰
シグマ・プロット 曲線フィットと回帰
カーブフィッティングとは、一連のデータ点と、場合によってはその他の制約条件にマッチする曲線を見つけることである。
科学者やエンジニアが、データの形状や挙動を最もよく表す曲線を視覚化し、プロットするために最もよく使用される。
- 回帰手順は、グラフにすると直線、平面、または曲線になる独立変数と従属変数の間の関連を見つける。
- 独立変数は既知の変数、つまり予測変数である。 これらはほとんどの場合、X軸の値です。 従属変数は応答変数とも呼ばれ、ほとんどの場合Y軸の値です。
- 回帰は、従属変数の値を予測するために1つ以上の独立変数の値を使用して、実際のデータを最も密接に記述する、またはフィットする方程式を見つける。 得られた方程式を元のデータ上にプロットすることで、データにフィットする曲線を作成することができる。
ダイナミックカーブフィッティング
非線形カーブフィッティングは、可能な限り最良の解を見つけるために収束する反復プロセスである。 パラメータの推測から始まり、方程式がどの程度フィットするかをチェックし、残差平方和の差が有意に減少しなくなるまで、より良い推測を続ける。 複雑な曲線フィットの問題には、SigmaPlotのダイナミックフィットウィザードを使用して、最適な解決策を見つけることができます。
- ダイナミックフィットウィザードは、可能な限り最良の解に収束する初期パラメータ値の探索を自動化します。
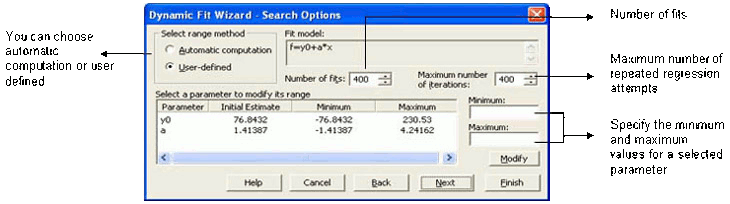
- 回帰ウィザードと同様に、ダイナミック・フィット・ウィザードは、カーブ・フィットの手順をステップ・バイ・ステップでガイドしますが、検索オプションを設定するパネルが追加されています(下図)。
ダイナミック・フィット・ウィザードは、パラメータが3つ以上あり、データ・ポイントに大きなばらつきがある可能性のある、より困難なカーブ・フィッティングの問題に特に役立ちます。 線形回帰や、単純な指数2パラメータ・フィットのようなそれほど難しくない問題では、ダイナミック・フィット・ウィザードはやりすぎで、回帰ウィザードを使うべきです。
ダイナミックフィットウィザードを使用する:
- 測定ノイズの除去
- 1つまたは複数の測定値が欠落している、または不適切に記録されている場合など、欠落しているデータポイントを埋める。
- 測定と測定の間の時間が十分に短くない場合など、データポイント間のデータを推定する補間。
- 測定値の前後のデータ値を探すなど、データポイントを超えてデータを推定すること。
- 離散データを多項式でモデル化し、得られた多項式方程式を微分することによってデータポイントの微分を求めるなど、デジタルデータを微分する。
- 曲線の離散点しかない場合に、曲線の下の面積を求めるなど、デジタルデータを統合する。
- 一次微分である速度、または二次微分である加速度の離散測定に基づいて、物体の軌道を求める。
SigmaPlotを使用した曲線フィッティングがいかに簡単であるかについての、より多くの技術的な情報と例へのリンク
