405 Waverley St Palo Alto
西格玛绘图 曲线拟合和回归
西格玛绘图 曲线拟合和回归
曲线拟合是找到一条与一系列数据点以及其他可能的限制条件相匹配的曲线。
科学家和工程师最常用它来可视化和绘制最能描述数据形状和行为的曲线。
- 回归程序是在自变量和因变量之间找到一种关联，这种关联在绘制图形时会产生一条直线、平面或曲线。
- 自变量是已知变量或预测变量。 这些通常是 X 轴的数值。 因变量也称为响应变量，通常是 Y 轴的数值。
- 回归利用一个或多个自变量的值来预测因变量的值，从而找到最接近或最适合实际数据的等式。 然后，可以将得到的方程绘制在原始数据上，生成一条符合数据的曲线。
动态曲线拟合
非线性曲线拟合是一个迭代过程，可能会收敛以找到最佳可能的解决方案。 它从猜测参数开始，检查方程的拟合程度，然后继续做出更好的猜测，直到残差平方和之间的差异不再显著减小。 对于复杂的曲线拟合问题，可使用 SigmaPlot 的动态拟合向导找到最佳解决方案。
- 动态拟合向导可自动搜索初始参数值，从而收敛到最佳解决方案。
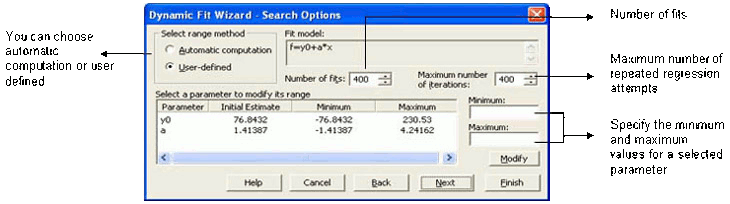
- 与回归向导一样，动态拟合向导也是曲线拟合程序的逐步指导，但多了一个用于设置搜索选项的面板（如下图）。
请注意，动态拟合向导尤其适用于难度较大的曲线拟合问题，这些问题涉及三个或更多参数，而且数据点的变异性可能很大。 对于线性回归或难度较低的问题，如简单的指数双参数拟合，动态拟合向导就显得多余了，您应该使用回归向导。
使用动态拟合向导
- 消除测量噪音
- 填补缺失的数据点，如一个或多个测量点缺失或记录不当
- 内插法，即在数据点之间估算数据，例如在测量时间间隔不够小的情况下
- 外推法，即估计数据点以外的数据，例如寻找测量之前或之后的数据值
- 微分数字数据，例如用多项式模拟离散数据并微分得到的多项式方程，从而求出数据点的导数
- 整合数字数据，例如在只有曲线离散点的情况下求得曲线下的面积
- 根据对物体速度（一导数）或加速度（二导数）的离散测量，获取物体的运动轨迹
更多技术信息链接，以及如何使用 SigmaPlot 轻松进行曲线拟合的示例