جرافيتي ذ.م.م
ميزات جديدة
في عام 2007، تم دمج وظائف وميزات SigmaStat في SigmaPlot بدءًا من الإصدار 11. ومع ذلك، في 1 فبراير 2016، تم إصدار SigmaStat 4.0 وهو متوفر الآن كمنتج مستقل.
فيما يلي التحسينات العديدة التي تم إدخالها على وظائف التحليل الإحصائي في SigmaStat:
- تحليل المكونات الرئيسية (PCA) - تحليل المكونات الرئيسية هو أسلوب لتقليل تعقيد البيانات عالية الأبعاد عن طريق تقريب البيانات بأبعاد أقل.
- تحليل التباين (ANCOVA) - تحليل التباين هو امتداد لتحليل التباين (ANOVA) الذي يتم الحصول عليه عن طريق تحديد واحد أو أكثر من المتغيرات المشتركة كمتغيرات إضافية في النموذج.
- انحدار كوكس – يتضمن هذا نموذج المخاطر النسبية مع التقسيم الطبقي لدراسة تأثير عوامل الخطر المحتملة على وقت بقاء السكان على قيد الحياة. يمكن أن تكون بيانات الإدخال قاطعة.
- اختبار T لعينة واحدة – يختبر الفرضية القائلة بأن متوسط السكان يساوي قيمة محددة.
- اختبارات نسبة الأرجحية والمخاطر النسبية – كلاهما يختبران الفرضية القائلة بأن العلاج ليس له أي تأثير على معدل حدوث بعض الأحداث المحددة في مجتمع ما. يتم استخدام نسبة الأرجحية في الدراسات بأثر رجعي لتحديد تأثير العلاج بعد ملاحظة الحدث. يتم استخدام المخاطر النسبية في الدراسات المستقبلية حيث تم اختيار مجموعات العلاج والسيطرة قبل وقوع الحدث.
- اختبار شابيرو-ويلك للحياة الطبيعية – اختبار أكثر دقة من اختبار كولموجوروف-سميرنوف لتقييم الحالة الطبيعية للبيانات التي تم أخذ عينات منها. يُستخدم في التحقق من الافتراضات في العديد من الاختبارات الإحصائية، ولكن يمكن استخدامه أيضًا مباشرةً في بيانات ورقة العمل.
- رسم بياني جديد للنتائج - مخططات ملف تعريف ANOVA: يُستخدم لتحليل التأثيرات الرئيسية والتفاعلات ذات الترتيب الأعلى للعوامل في تصميم ANOVA متعدد العوامل من خلال مقارنة متوسطات أقل الوسائل المربعة.
- تحويلات احتمالية جديدة – تمت إضافة أربع وثلاثين وظيفة جديدة إلى لغة التحويل الخاصة بـ SigmaStat لحساب الاحتمالات والنتائج المرتبطة بالتوزيعات التي تنشأ في العديد من مجالات الدراسة.
- تغيير جديد في الواجهة - الانحدار غير الخطي: واجهة معالج سهلة الاستخدام وتقارير أكثر تفصيلاً.
- تغيير الواجهة الجديد - التحويلات السريعة: طريقة أسهل لإجراء العمليات الحسابية في ورقة العمل.
- تغيير الواجهة الجديدة - واجهة المستخدم الجديدة: تتيح للمستخدم العمل بسهولة أكبر مع أوراق عمل Excel.
- تمت إضافة تصحيح ييتس إلى اختبار مان ويتني - يتم استخدام تصحيح ييتس للاستمرارية، أو اختبار مربع كاي ييتس عند اختبار الاستقلال في جدول الطوارئ عند تقييم ما إذا كانت عينتان من الملاحظات تأتي من نفس التوزيع.
- تحسين رسائل الخطأ - أضافت رسائل الخطأ المحسنة معلومات عند فشل التحقق من الافتراضات لـ ANOVA.
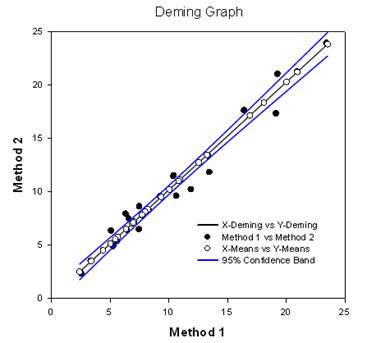
- انحدار ديمينج - يسمح انحدار ديمينج بوجود أخطاء في كل من المتغيرات X وY - وهي تقنية لمقارنة الطرق حيث تكون بيانات X من إحدى الطرق وبيانات y من الطريقة الأخرى. تعمل طريقة انحدار ديمنج بشكل أساسي على توسيع الانحدار الخطي العادي، حيث تعتبر قيم X خالية من الأخطاء، إلى الحالة التي يكون فيها خطأ في كل من X وY (كلا الطريقتين). يمكن بعد ذلك اختبار الفرضيات، بميل مختلف عن 1.0 على سبيل المثال، لتحديد ما إذا كانت الطرق هي نفسها. على سبيل المثال، يمكن استخدامه لمقارنة أداتين مصممتين لقياس نفس المادة أو لمقارنة طريقتين خوارزميتين للكشف عن الأورام في الصور. يقارن الرسم البياني بين الطريقتين لتحديد ما إذا كانتا مختلفتين أم متماثلتين. تقرير يعطي نتائج إحصائية.
- معيار معلومات Akaike (AICc) - معيار معلومات Akaike متوفر الآن في تقارير الانحدار غير الخطية. إنه معيار الملاءمة الذي يفسر أيضًا عدد المعلمات في المعادلة. كما أنها صالحة للمعادلات غير المتداخلة التي تحدث، على سبيل المثال، في تحليلات حركية الإنزيم.
- وظائف احتمالية جديدة للانحدار غير الخطي - تمت إضافة إجمالي 24 دالة احتمالية إلى مكتبة المنحنى الملائمة. تم إنشاء معادلات تقدير المعلمات الأولية التلقائية لكل منها.
- ترجيح الانحدار غير الخطي - توجد الآن سبع وظائف ترجيح مختلفة مدمجة في كل معادلة انحدار غير خطية (تختلف الأبعاد الثلاثية قليلاً). هذه الوظائف هي متبادل y، متبادل y تربيع، مقلوب x، مقلوب x تربيع، توقعات متبادلة، توقعات متبادلة تربيعية و كوشي. يتم استخدام خوارزمية المربعات الصغرى المعاد وزنها بشكل متكرر للسماح بتغيير الأوزان أثناء كل تكرار انحدار غير خطي.
- تحسينات اختبار المقارنة المتعددة - تم إجراء تحسينين مهمين. تمت إضافة قيم P لنتائج ANOVA غير المعلمية. هذه لم تكن موجودة من قبل. أيضًا، اقتصرت قيم P المقارنة المتعددة على اختيارات منفصلة (0.05، 0.01، وما إلى ذلك). لم يعد هذا القيد موجودًا ويمكن استخدام أي قيمة P صالحة.
الاختبارات الإحصائية الرئيسية الجديدة
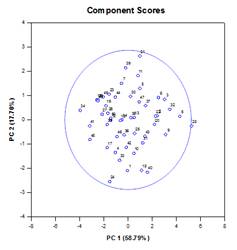
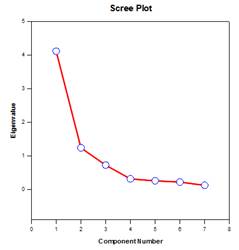
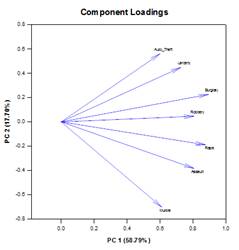
تحليل المكونات الرئيسية (PCA) – تحليل المكونات الرئيسية هو أسلوب لتقليل تعقيد البيانات عالية الأبعاد عن طريق تقريب البيانات بأبعاد أقل. ويسمى كل بعد جديد مكونًا رئيسيًا ويمثل مزيجًا خطيًا من المتغيرات الأصلية. يمثل المكون الرئيسي الأول أكبر قدر ممكن من الاختلاف في البيانات. يمثل كل مكون رئيسي لاحق أكبر قدر ممكن من التباين المتبقي ويكون متعامدًا مع جميع المكونات الرئيسية السابقة.
يمكنك فحص المكونات الرئيسية لفهم مصادر الاختلاف في بياناتك. يمكنك أيضًا استخدامها في تكوين نماذج تنبؤية. إذا كان معظم الاختلاف في بياناتك موجودًا في مجموعة فرعية منخفضة الأبعاد، فقد تتمكن من تصميم متغير الاستجابة الخاص بك من حيث المكونات الرئيسية. يمكنك استخدام المكونات الأساسية لتقليل عدد المتغيرات في الانحدار والتجميع والتقنيات الإحصائية الأخرى. الهدف الأساسي لتحليل المكونات الرئيسية هو شرح مصادر التباين في البيانات وتمثيل البيانات بمتغيرات أقل مع الحفاظ على معظم التباين الإجمالي.
أمثلة على الرسوم البيانية للمكونات الرئيسية:
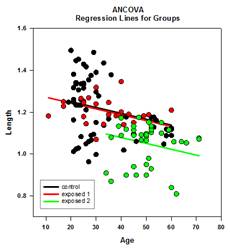
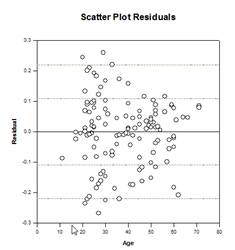
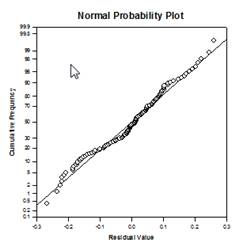
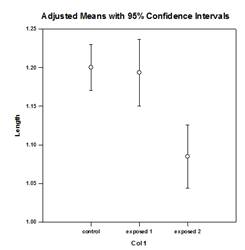
تحليل التباين (ANCOVA) – تحليل التباين هو امتداد لتحليل التباين الذي يتم الحصول عليه عن طريق تحديد واحد أو أكثر من المتغيرات المشتركة كمتغيرات إضافية في النموذج. إذا قمت بترتيب بيانات تحليل التباين (ANCOVA) في ورقة عمل SigmaPlot باستخدام تنسيق البيانات المفهرسة ، فسيمثل عمود واحد العامل وسيمثل عمود واحد المتغير التابع (الملاحظات) كما في تصميم تحليل التباين (ANOVA). بالإضافة إلى ذلك، سيكون لديك عمود واحد لكل متغير مشترك.
أمثلة على الرسوم البيانية ANCOVA:
ميزات إحصائية جديدة
 على سبيل المثال، يحتوي الملف المناسب لوظيفة الكثافة اللوغاريتمية الطبيعية على معادلة الكثافة اللوغاريتمية الطبيعية lognormden(x,a,b)، ومعادلات لتقدير المعلمة الأولية التلقائية ووظائف الترجيح السبع الجديدة.
[Variables]
س = العمود (1)
ص = العمود (2)
reciprocal_y = 1/abs(y)
reciprocal_ysquare = 1/y^2
reciprocal_x = 1/أبس(س)
reciprocal_xsquare = 1/x^2
reciprocal_pred = 1/أبس(و)
reciprocal_predsqr = 1/f^2
الوزن_كوشي = 1/(1+4*(yf)^2)
‘وظائف تقدير المعلمة الأولية التلقائية
فخ(ف,ص)=.5*المجموع(({0,q}+{q,0})[data(2,size(q))] *فرق (ص)[data(2,size(r))] )
الصورة = فرز (معقد (س، ص)، س)
u = كتلة فرعية(s,1,1,1, size(x))
v = كتلة فرعية(s,2,1,2, size(y))
أعني = فخ (u*v،u)
varest=فخ((u-الأسوء)^2*v,u)
ع = 1 + أفاريست / أتعس ^ 2
[Parameters]
أ= إذا (أعني> 0, قانون الجنسية (يعني/جذر(ع)), 0)
ب = إذا (ص> = 1، الجذر التربيعي (ln(p)))، 1)
[Equation]
f=lognormden(x,a,b)
تناسب f إلى y
”تناسب f إلى y مع الوزن المتبادل_y
”تناسب f إلى y مع الوزن reciprocal_ysquare
”تناسب f إلى y مع الوزن reciprocal_x
”تناسب f إلى y مع الوزن reciprocal_xsquare
”تناسب f إلى y مع الوزن المتبادل
”تناسب f إلى y مع الوزن reciprocal_predsqr
”تناسب f إلى y مع الوزن Weight_Cauchy
[Constraints]
ب> 0
[Options]
التسامح = 1e-010
حجم الخطوات = 1
التكرارات = 200
وظائف الوزن في الانحدار غير الخطي – تستخدم عناصر معادلة SigmaPlot أحيانًا متغير وزن بغرض تعيين وزن لكل ملاحظة (أو استجابة) في مجموعة بيانات الانحدار. يقيس وزن الملاحظة عدم اليقين بالنسبة للتوزيع الاحتمالي الذي تم أخذ العينات منه. يشير الوزن الأكبر إلى ملاحظة تختلف قليلًا عن المتوسط الحقيقي لتوزيعها بينما يشير الوزن الأصغر إلى ملاحظة تم أخذ عينات منها أكثر من ذيل توزيعها.
في ظل الافتراضات الإحصائية لتقدير معلمات النموذج المناسب باستخدام نهج المربعات الصغرى، تكون الأوزان، حتى عامل القياس، مساوية لمقلوب التباينات السكانية للتوزيعات (الغاوسية) التي تم أخذ عينات منها الملاحظات. هنا، نحدد المتبقي ، والذي يسمى أحيانًا الخام المتبقي ، على أنه الفرق بين الملاحظة والقيمة المتوقعة (قيمة النموذج المناسب) عند قيمة معينة للمتغير (المتغيرات) المستقل. إذا كانت تباينات الملاحظات ليست كلها متماثلة ( تغايرية) ، فستكون هناك حاجة إلى متغير وزن ويتم حل مشكلة المربعات الصغرى الموزونة لتقليل المجموع المرجح لمربعات البقايا للعثور على أفضل المعلمات المناسبة.
ستسمح ميزتنا الجديدة للمستخدم بتحديد متغير الوزن كدالة للمعلمات الموجودة في النموذج المناسب. تمت إضافة سبع وظائف وزن محددة مسبقًا إلى كل وظيفة مناسبة (تختلف الوظائف ثلاثية الأبعاد قليلاً). السبعة الموضحة أدناه هي 1/y، 1/y 2 ، 1/x، 1/x 2 ، 1/متوقع، 1/متنبأ 2 وكوشي.
على سبيل المثال، يحتوي الملف المناسب لوظيفة الكثافة اللوغاريتمية الطبيعية على معادلة الكثافة اللوغاريتمية الطبيعية lognormden(x,a,b)، ومعادلات لتقدير المعلمة الأولية التلقائية ووظائف الترجيح السبع الجديدة.
[Variables]
س = العمود (1)
ص = العمود (2)
reciprocal_y = 1/abs(y)
reciprocal_ysquare = 1/y^2
reciprocal_x = 1/أبس(س)
reciprocal_xsquare = 1/x^2
reciprocal_pred = 1/أبس(و)
reciprocal_predsqr = 1/f^2
الوزن_كوشي = 1/(1+4*(yf)^2)
‘وظائف تقدير المعلمة الأولية التلقائية
فخ(ف,ص)=.5*المجموع(({0,q}+{q,0})[data(2,size(q))] *فرق (ص)[data(2,size(r))] )
الصورة = فرز (معقد (س، ص)، س)
u = كتلة فرعية(s,1,1,1, size(x))
v = كتلة فرعية(s,2,1,2, size(y))
أعني = فخ (u*v،u)
varest=فخ((u-الأسوء)^2*v,u)
ع = 1 + أفاريست / أتعس ^ 2
[Parameters]
أ= إذا (أعني> 0, قانون الجنسية (يعني/جذر(ع)), 0)
ب = إذا (ص> = 1، الجذر التربيعي (ln(p)))، 1)
[Equation]
f=lognormden(x,a,b)
تناسب f إلى y
”تناسب f إلى y مع الوزن المتبادل_y
”تناسب f إلى y مع الوزن reciprocal_ysquare
”تناسب f إلى y مع الوزن reciprocal_x
”تناسب f إلى y مع الوزن reciprocal_xsquare
”تناسب f إلى y مع الوزن المتبادل
”تناسب f إلى y مع الوزن reciprocal_predsqr
”تناسب f إلى y مع الوزن Weight_Cauchy
[Constraints]
ب> 0
[Options]
التسامح = 1e-010
حجم الخطوات = 1
التكرارات = 200
وظائف الوزن في الانحدار غير الخطي – تستخدم عناصر معادلة SigmaPlot أحيانًا متغير وزن بغرض تعيين وزن لكل ملاحظة (أو استجابة) في مجموعة بيانات الانحدار. يقيس وزن الملاحظة عدم اليقين بالنسبة للتوزيع الاحتمالي الذي تم أخذ العينات منه. يشير الوزن الأكبر إلى ملاحظة تختلف قليلًا عن المتوسط الحقيقي لتوزيعها بينما يشير الوزن الأصغر إلى ملاحظة تم أخذ عينات منها أكثر من ذيل توزيعها.
في ظل الافتراضات الإحصائية لتقدير معلمات النموذج المناسب باستخدام نهج المربعات الصغرى، تكون الأوزان، حتى عامل القياس، مساوية لمقلوب التباينات السكانية للتوزيعات (الغاوسية) التي تم أخذ عينات منها الملاحظات. هنا، نحدد المتبقي ، والذي يسمى أحيانًا الخام المتبقي ، على أنه الفرق بين الملاحظة والقيمة المتوقعة (قيمة النموذج المناسب) عند قيمة معينة للمتغير (المتغيرات) المستقل. إذا كانت تباينات الملاحظات ليست كلها متماثلة ( تغايرية) ، فستكون هناك حاجة إلى متغير وزن ويتم حل مشكلة المربعات الصغرى الموزونة لتقليل المجموع المرجح لمربعات البقايا للعثور على أفضل المعلمات المناسبة.
ستسمح ميزتنا الجديدة للمستخدم بتحديد متغير الوزن كدالة للمعلمات الموجودة في النموذج المناسب. تمت إضافة سبع وظائف وزن محددة مسبقًا إلى كل وظيفة مناسبة (تختلف الوظائف ثلاثية الأبعاد قليلاً). السبعة الموضحة أدناه هي 1/y، 1/y 2 ، 1/x، 1/x 2 ، 1/متوقع، 1/متنبأ 2 وكوشي.
 أحد تطبيقات هذا الترجيح التكيفي الأكثر عمومية هو في المواقف التي لا يمكن فيها تحديد تباينات الملاحظات قبل إجراء الملاءمة. على سبيل المثال، إذا كانت جميع الملاحظات موزعة بواسون، فإن متوسط عدد السكان، وهو ما تقدره القيم المتوقعة، يساوي تباينات المجتمع. على الرغم من أن أسلوب المربعات الصغرى لتقدير المعلمات مصمم للبيانات الموزعة بشكل طبيعي، إلا أنه يتم استخدام توزيعات أخرى أحيانًا مع المربعات الصغرى عندما لا تتوفر طرق أخرى. في حالة بيانات بواسون ، نحتاج إلى تعريف متغير الوزن باعتباره مقلوب القيم المتوقعة. يُشار إلى هذا الإجراء أحيانًا باسم “الترجيح بالقيم المتوقعة”.
تطبيق آخر للترجيح التكيفي هو الحصول على إجراءات قوية لتقدير المعلمات التي تخفف من آثار القيم المتطرفة. في بعض الأحيان، قد يكون هناك عدد قليل من الملاحظات في مجموعة البيانات التي يتم أخذ عينات منها من ذيل توزيعاتها باحتمالية صغيرة، أو هناك عدد قليل من الملاحظات التي يتم أخذ عينات منها من توزيعات تنحرف قليلاً عن افتراض الحالة الطبيعية المستخدم في تقدير المربعات الصغرى وبالتالي تلوث مجموعة البيانات. هذه الملاحظات الشاذة، والتي تسمى القيم المتطرفة في متغير الاستجابة ، يمكن أن يكون لها تأثير كبير على نتائج الملاءمة لأنها تحتوي على بقايا كبيرة نسبيًا (خام أو مرجح) وبالتالي تضخم مجموع المربعات التي يتم تقليلها.
تتمثل إحدى طرق التخفيف من آثار القيم المتطرفة في استخدام متغير الوزن الذي يمثل دالة للقيم المتبقية (وبالتالي، أيضًا وظيفة للمعلمات)، حيث يرتبط الوزن المخصص للملاحظة عكسيًا بحجم المتبقي. يعتمد تعريف وظيفة الترجيح المستخدمة على افتراضات حول توزيعات الملاحظات (بافتراض أنها ليست طبيعية) ومخطط لتحديد حجم المتبقي الذي يجب تحمله. يتم تعريف دالة الترجيح كوشي من حيث القيم المتبقية، yf حيث y هي قيمة المتغير التابع وf هي الدالة الملائمة، ويمكن استخدامها لتقليل تأثير القيم المتطرفة.
الوزن_كوشي = 1/(1+4*(yf)^2)
تعتمد خوارزمية تقدير المعلمة التي نستخدمها للترجيح التكيفي، والمربعات الصغرى المعاد وزنها بشكل متكرر (IRLS)، على حل سلسلة من مشاكل المربعات الصغرى ذات الوزن الثابت حيث يتم حل كل مشكلة فرعية باستخدام تطبيقنا الحالي لخوارزمية Levenberg-Marquardt . تبدأ هذه العملية بتقييم الأوزان باستخدام قيم المعلمات الأولية ثم تقليل مجموع المربعات بهذه الأوزان الثابتة. يتم بعد ذلك استخدام المعلمات الأكثر ملائمة لإعادة تقييم الأوزان.
باستخدام قيم الوزن الجديدة، يتم تكرار العملية المذكورة أعلاه لتقليل مجموع المربعات. ونستمر على هذا المنوال حتى يتحقق التقارب. المعيار المستخدم للتقارب هو أن يكون الخطأ النسبي بين الجذر التربيعي لمجموع البقايا المرجحة لقيم المعلمات الحالية والجذر التربيعي لمجموع البقايا المرجحة لقيم معلمات التكرار السابق أقل من قيمة التسامح المنصوص عليها في عنصر المعادلة. وكما هو الحال مع إجراءات التقدير الأخرى، فإن التقارب غير مضمون.
أحد تطبيقات هذا الترجيح التكيفي الأكثر عمومية هو في المواقف التي لا يمكن فيها تحديد تباينات الملاحظات قبل إجراء الملاءمة. على سبيل المثال، إذا كانت جميع الملاحظات موزعة بواسون، فإن متوسط عدد السكان، وهو ما تقدره القيم المتوقعة، يساوي تباينات المجتمع. على الرغم من أن أسلوب المربعات الصغرى لتقدير المعلمات مصمم للبيانات الموزعة بشكل طبيعي، إلا أنه يتم استخدام توزيعات أخرى أحيانًا مع المربعات الصغرى عندما لا تتوفر طرق أخرى. في حالة بيانات بواسون ، نحتاج إلى تعريف متغير الوزن باعتباره مقلوب القيم المتوقعة. يُشار إلى هذا الإجراء أحيانًا باسم “الترجيح بالقيم المتوقعة”.
تطبيق آخر للترجيح التكيفي هو الحصول على إجراءات قوية لتقدير المعلمات التي تخفف من آثار القيم المتطرفة. في بعض الأحيان، قد يكون هناك عدد قليل من الملاحظات في مجموعة البيانات التي يتم أخذ عينات منها من ذيل توزيعاتها باحتمالية صغيرة، أو هناك عدد قليل من الملاحظات التي يتم أخذ عينات منها من توزيعات تنحرف قليلاً عن افتراض الحالة الطبيعية المستخدم في تقدير المربعات الصغرى وبالتالي تلوث مجموعة البيانات. هذه الملاحظات الشاذة، والتي تسمى القيم المتطرفة في متغير الاستجابة ، يمكن أن يكون لها تأثير كبير على نتائج الملاءمة لأنها تحتوي على بقايا كبيرة نسبيًا (خام أو مرجح) وبالتالي تضخم مجموع المربعات التي يتم تقليلها.
تتمثل إحدى طرق التخفيف من آثار القيم المتطرفة في استخدام متغير الوزن الذي يمثل دالة للقيم المتبقية (وبالتالي، أيضًا وظيفة للمعلمات)، حيث يرتبط الوزن المخصص للملاحظة عكسيًا بحجم المتبقي. يعتمد تعريف وظيفة الترجيح المستخدمة على افتراضات حول توزيعات الملاحظات (بافتراض أنها ليست طبيعية) ومخطط لتحديد حجم المتبقي الذي يجب تحمله. يتم تعريف دالة الترجيح كوشي من حيث القيم المتبقية، yf حيث y هي قيمة المتغير التابع وf هي الدالة الملائمة، ويمكن استخدامها لتقليل تأثير القيم المتطرفة.
الوزن_كوشي = 1/(1+4*(yf)^2)
تعتمد خوارزمية تقدير المعلمة التي نستخدمها للترجيح التكيفي، والمربعات الصغرى المعاد وزنها بشكل متكرر (IRLS)، على حل سلسلة من مشاكل المربعات الصغرى ذات الوزن الثابت حيث يتم حل كل مشكلة فرعية باستخدام تطبيقنا الحالي لخوارزمية Levenberg-Marquardt . تبدأ هذه العملية بتقييم الأوزان باستخدام قيم المعلمات الأولية ثم تقليل مجموع المربعات بهذه الأوزان الثابتة. يتم بعد ذلك استخدام المعلمات الأكثر ملائمة لإعادة تقييم الأوزان.
باستخدام قيم الوزن الجديدة، يتم تكرار العملية المذكورة أعلاه لتقليل مجموع المربعات. ونستمر على هذا المنوال حتى يتحقق التقارب. المعيار المستخدم للتقارب هو أن يكون الخطأ النسبي بين الجذر التربيعي لمجموع البقايا المرجحة لقيم المعلمات الحالية والجذر التربيعي لمجموع البقايا المرجحة لقيم معلمات التكرار السابق أقل من قيمة التسامح المنصوص عليها في عنصر المعادلة. وكما هو الحال مع إجراءات التقدير الأخرى، فإن التقارب غير مضمون. 