一般的な特徴
新機能
2007年、SigmaStatの機能と特徴はバージョン11からSigmaPlotに統合されました。 しかし、2016年2月1日にSigmaStat 4.0がリリースされ、スタンドアロン製品として利用できるようになった。
以下はSigmaStatの統計解析機能に対する多くの改良点です:
- 主成分分析(PCA) - 主成分分析は、より少ない次元でデータを近似することにより、高次元データの複雑さを軽減するための手法です。
- 共分散分析 (ANCOVA) - 共分散分析は,1つまたは複数の共変量をモデル中の追加変数として指定することによって得られるANOVA (分散分析)の拡張である.
- Cox 回帰 - これは、集団の生存時間に対する潜在的リスク因子の影響を調査するための層別化を伴う比例ハザード・モデルを含む。 入力データはカテゴリカルでもよい。
- 1標本のT検定 - 母集団の平均が指定された値に等しいという仮説を検定する。
- オッズ比検定と相対リスク検定 - 両方とも、ある治療が集団におけるある特定の事象の発生率に影響を与えないという仮説を検定する。 オッズ比は、事象が観察された後に治療効果を判定するためにレトロスペクティブ研究で使用される。 相対リスクは、治療群と対照群がイベント発生前に選択されている前向き研究で使用される。
- シャピロ・ウィルク正規性検定 - サンプル・データの正規性を評価するためのコルモゴロフ・スミルノフよりも正確な検定。 多くの統計検定の仮定チェックで使用されるが、ワークシートのデータで直接使用することもできる。
- 新しい結果グラフ - ANOVA プロファイル・プロット.最小2乗平均の平均を比較することにより、多因子ANOVAデザインにおける因子の主効果および高次交互作用を分析するために使用される。
- 新しい確率変換 - SigmaStatの変換言語に34の新しい関数が追加され、多くの研究分野で発生する分布に関連する確率と得点を計算できるようになりました。
- 新しいインターフェースの変更 - 非線形回帰:使いやすいウィザードインターフェイスとより詳細なレポート。
- 新しいインターフェイスの変更 - クイック変換:ワークシートで計算を実行する簡単な方法です。
- 新しいインターフェイスの変更 - 新しいユーザーインターフェイス:Excelワークシートをより簡単に操作できます。
- Mann-Whitney 検定に追加されたYates 補正 - 連続性のためのYates 補正、またはYates カイ2乗検定は、オブザベーションの2つの標本が同じ分布から来たかどうかを評価するとき、分割表で独立性を検定するときに使用される。
- エラーメッセージの改善 - ANOVAの仮定チェックが失敗した場合のエラーメッセージが改善されました。
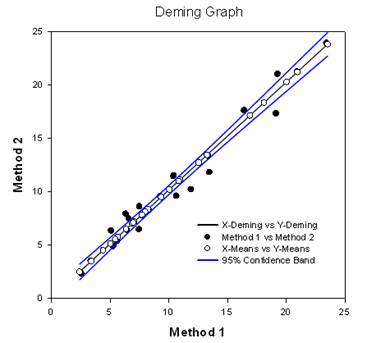
- デミング回帰 - デミング回帰は、X変数とY変数の両方の誤差を許容する - Xデータが1つの方法から、Yデータがもう1つの方法からの方法比較のためのテクニック。 デミング回帰法は,基本的に,X値に誤差がないとみなされる通常の線形回帰を,XとY(両方の方法)の両方に誤差がある場合に拡張する. そして、例えば1.0と異なる傾きなどの仮説を検証し、方法が同じかどうかを判断することができる。 例えば、同じ物質を測定するために設計された2つの機器を比較したり、画像中の腫瘍を検出するための2つのアルゴリズム手法を比較したりするのに使われるかもしれない。 グラフは、2つの方法が異なるか同じかを判断するために比較したものである。 レポートは統計的な結果を示す。
- 赤池情報量規準 (AICc) - 赤池情報量規準が非線形回帰レポートで利用できるようになりました。 これは、方程式のパラメータ数も考慮した適合度基準である。 また、例えば酵素の速度論的分析に見られるような、入れ子式でない方程式にも有効である。
- 非線形回帰のための新しい確率関数 - 合計24の確率関数がカーブフィットライブラリに追加されました。 それぞれ自動初期パラメータ推定式が作成されている。
- 非線形回帰の重み付け - 各非線形回帰式に組み込まれた7つの異なる重み付け関数がある(3Dは若干異なる)。 これらの関数は、yの逆数、yの2乗の逆数、xの逆数、xの2乗の逆数、predictedsの逆数、predictedsの2乗の逆数、Caucyの逆数である。 反復再重み付け最小2乗法は、各非線形回帰の反復中に重みを変更できるようにするために使用される。
- 複数比較テストの改善 - 2つの重要な改善がなされた。 ノンパラメトリックANOVAの結果のP値を追加した。 これらは以前には存在しなかった。 また、多重比較のP値は離散的な選択(0.05、0.01など)に限定された。 この制限はもはや存在せず、どのような有効なP値でも使用することができる。
主な新しい統計的検定
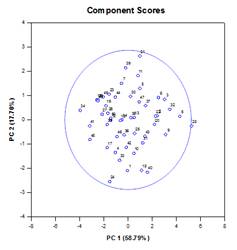
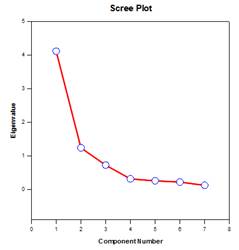
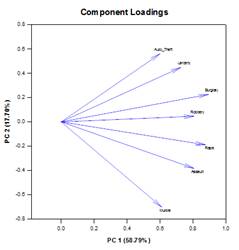
主成分分析(PCA) – 主成分分析は、より少ない次元でデータを近似することにより、高次元データの複雑さを軽減するための手法です。 それぞれの新しい次元は主成分と呼ばれ、元の変数の線形結合を表す。 第1主成分は、データのばらつきを可能な限り考慮する。 後続の各主成分は、残りの変動のできるだけ多くを説明し、前のすべての主成分と直交する。
主成分を調べることで、データのばらつきの原因を理解することができます。 また、予測モデルを作成する際にも使用できる。 データの変動のほとんどが低次元の部分集合に存在する場合、主成分の観点から応答変数をモデル化できるかもしれません。 主成分は、回帰、クラスタリング、その他の統計的手法において、変数の数を減らすために使用することができます。 主成分分析の主な目的は、データの変動の原因を説明し、全分散の大部分を保持しながら、より少ない変数でデータを表現することです。
主成分グラフの例:
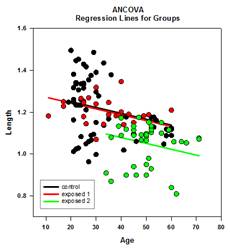
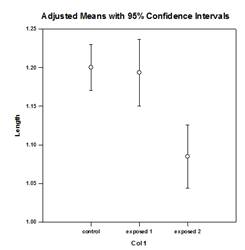
共分散分析 (ANCOVA) – 共分散分析は,1つまたは複数の共変量をモデル中の追加変数として指定することによって得られるANOVAの拡張である. インデックス付きデータ形式を用いてANCOVAデータをSigmaPlotワークシートに配置すると、1列がANOVAデザインと同じように因子を表し、1列が従属変数(オブザベーション)を表します。 さらに、共変量ごとに1つの列ができます。
ANCOVAグラフの例
新しい統計機能
多重比較の改善 – 重複比較のP値計算が大幅に改善されました。 以下の多重比較手続き、Tukey(ノンパラメトリック検定)、SNK(ノンパラメトリック検定)、Dunnettの、Dunnの(ノンパラメトリックのみ)、Duncanは、分析的にp値を計算するのではなく、計算された検定統計量が群平均の有意差を表しているかどうかを、必要に応じて補間を用いて決定するために、特定の分布の臨界値のルックアップテーブルを使用した。 したがって、これらの検定ではp値は報告されず、有意差が存在するかどうかの結論のみが報告された。 この方法の大きな問題は、ルックアップテーブルが0.05と0.01の2つの有意水準でしか利用できないことである。 もう一つの問題は、多くの顧客がp値を知りたがることだ。 SigmaPlotでは、すべてのポストホック手続きの検定統計量の分布を計算するアルゴリズムがコード化され、ルックアップテーブルは廃止されました。 その結果、すべてのpost-hoc手続きの調整されたp値がレポートに掲載されるようになった。 また、多重比較の有意水準を.05や.01に制限する必要もなくなった。 その代わりに、多重比較の有意水準は、メイン(オムニバス)検定の有意水準と同じになる。 このp値に制限はなく、どのような有効な値を用いてもよい。
赤池情報量規準 (AICc) – 赤池情報量規準が回帰ウィザードと動的フィットウィザードのレポートとレポートオプションダイアログに追加されました。 これは、与えられたデータ集合に回帰モデルをフィッティングする際の相対的なパフォーマンスを測定する方法を提供する。 情報エントロピーの概念に基づくこの基準は、データを記述するためにモデルを使用する際に失われる情報の相対的な尺度を提供する。
より具体的には、推定モデルの尤度を最大化すること(データが正規分布している場合、残差平方和を最小化することと同じ)と、モデルの自由パラメータの数を最小に保ち、複雑さを軽減することのトレードオフを与える。 適合度はパラメータを増やすことでほとんどの場合改善されるが、過剰適合は入力データの変化に対するモデルの感度を上げ、予測能力を台無しにする。
AICを使用する基本的な理由は、モデル選択の指針としてである。 実際には、候補モデルの集合と与えられたデータセットに対して計算される。 AIC値が最小のモデルが、集合の中で「真の」モデルを最もよく表すモデル、つまりAICが推定するために設計された情報損失を最小化するモデルとして選択される。
最小のAICを持つモデルが決定された後、最小のAICを持つモデルに対して情報損失を減らす確率を測定するために、他の候補モデルの各々について相対尤度を計算することもできる。 相対尤度は、調査者がセット内の複数のモデルをさらに検討するために保持すべきかどうかを決定する際に役立ちます。
AICの計算は、Akaike1によって得られた以下の一般式に基づいている。
![]()
ここで、![]() はモデルの自由パラメーターの数であり、
はモデルの自由パラメーターの数であり、![]() は推定モデルの尤度関数の最大化値である。
は推定モデルの尤度関数の最大化値である。
データ![]() のサンプルサイズが、パラメータ
のサンプルサイズが、パラメータ![]() の数に対して小さい場合(著者によっては、
の数に対して小さい場合(著者によっては、![]() が
が![]() の数倍以下である場合)、AICはオーバーフィッティングから保護するために、それほどうまく機能しません。 この場合、AICの補正版が次のように与えられる:
の数倍以下である場合)、AICはオーバーフィッティングから保護するために、それほどうまく機能しません。 この場合、AICの補正版が次のように与えられる:
![]()
余分なパラメータがある場合、AICcはAICよりも大きなペナルティを課すことがわかる。 ほとんどの著者は、すべての状況においてAICの代わりにAICcを使うべきだという意見で一致しているようだ。
確率フィット関数– 24の新しい確率フィット関数がフィットライブラリstandard.jflに追加されました。 これらの関数と方程式、グラフの形を以下に示す:

例として、対数正規密度関数のフィットファイルには、対数正規密度lognormden(x,a,b)の式、自動初期パラメータ推定の式、7つの新しい重み付け関数が含まれています。
[Variables]
x = col(1)
y = col(2)
逆y = 1/abs(y)
逆二乗 = 1/y^2
逆数x = 1/abs(x)
逆2乗 = 1/x^2
reciprocal_pred = 1/abs(f)
レシプロ・プレッド・スクエア = 1/f^2
Weight_Cauchy = 1/(1+4*(y-f)^2)
自動初期パラメータ推定関数
trap(q,r)=.5*total(({0,q}+{q,0})[data(2,size(q))]*diff(r)[data(2,size(r))])
s=sort(complex(x,y),x)
u = サブブロック(s,1,1,1, size(x))
v = サブブロック(s,2,1,2, size(y))
meanest = trap(u*v,u)
varest=trap((u-meanest)^2*v,u)
p = 1+varest/meanest^2
[Parameters]
a= if(meanest> 0, ln(meanest/sqrt(p)), 0)
b= if(p>= 1, sqrt(ln(p)), 1)
[Equation]
f=lognormden(x,a,b)
yに合う
「yにfを重みreciprocal_yで当てはめる
「yにfを重み付きで当てはめる。
「yにfを重みの逆数xで当てはめる
「yにfを重み付きで当てはめる。
「fをyにフィットさせる。
「fをyにフィットさせる。
「重みweight_Cauchyでyにfを合わせる
[Constraints]
b>0
[Options]
公差=1e-010
stepize=1
反復=200
非線形回帰における重み関数– SigmaPlot 方程式の項目は、回帰データ集合の各オブザベーション(または応答)に重みを割り当てる目的で、重み変数を使うことがあります。 オブザベーションの重みは、それがサンプリングされた確率分布に対する不確実性を測定します。 より大きなウェイトは、その分布の真の平均からほとんど変化しないオブザベーションを示し、より小さなウェイトは、その分布のテールからより多くサンプリングされたオブザベーションを指す。
最小2乗アプローチを用いて適合モデルのパラメータを推定するための統計的仮定の下では,重みは,スケール・ファクターまで,オブザベーションがサンプリングされた(ガウス)分布の母分散の逆数に等しい. ここで、残差(生の残差と呼ばれることもある)を、独立変数の任意の値でのオブザベーションと予測値(適合モデルの値)の差と定義する。 オブザベーションの分散がすべて同じでない場合(異分散性)、重み変数が必要となり、残差の重み付き2乗和を最小化する重み付き最小2乗問題が、ベスト・フィット・パラメータを見つけるために解かれる。
新機能では、フィットモデルに含まれるパラメータの関数として重み変数を定義することができます。 各フィット関数には、あらかじめ定義された7つの重み関数が追加されている(3D関数は若干異なる)。 以下の7つは、1/y、1/y2、1/x、1/x2、1/predicted、1/predicteds2、Cauchyである。

このより一般的な適応重みづけの1つの応用は、適合を実行する前にオブザベーションの分散が決定できない状況である。 たとえば、すべてのオブザベーションがポアソン分布であれば、予測値が推定している母平均は母分散に等しい。 パラメータを推定するための最小二乗法は正規分布データ用に設計されているが、他の方法が利用できない場合、最小二乗法で他の分布が使われることもある。 ポアソン・データの場合、重み変数を予測値の逆数として定義する必要がある。 この手順は「予測値による重み付け」と呼ばれることもある。
適応的重み付けのもう一つの応用は、外れ値の影響を軽減するロバストなパラメータ推定手順を得ることである。 時折、小さな確率でそれらの分布の末尾からサンプリングされたデータ集合のオブザベーションがいくつかあったり、最小2乗推定で使用される正規性の仮定からわずかに逸脱した分布からサンプリングされたオブザベーションがいくつかあったりして、データ集合を汚染することがある。 応答変数の外れ値と呼ばれるこれらの異常なオブザベーションは、比較的大きな(生のまたは重みづけされた)残差を持ち、したがって最小化される平方和を増大させるので、適合結果に大きな影響を持つことがある。
外れ値の効果を緩和する1つの方法は、残差の関数(したがって、パラメータの関数でもある)である重み変数を使用することであり、ここでオブザベーションに割り当てられる重みは、残差のサイズに反比例する。 どのような重みづけ関数を使用するかの定義は、オブザベーションの分布に関する仮定(それらが正規分布でないと仮定する)、およびどの程度の残差を許容するかを決定するスキームに依存する。 コーシー重み付け関数は、残差y-f(yは従属変数値、fはフィッティング関数)で定義され、外れ値の影響を最小化するために使用できます。
Weight_Cauchy = 1/(1+4*(y-f)^2)
適応的重み付けに使用するパラメータ推定アルゴリズムである反復再重み付け最小二乗法(IRLS)は、定重み付け最小二乗法問題のシーケンスを解くことに基づいており、各サブ問題は現在実装しているレーベンバーグ・マルカールト・アルゴリズムを使用して解かれる。 このプロセスは、パラメータの初期値を用いて重みを評価し、その固定重みで平方和を最小化することから始まる。 そして、ベストフィットのパラメーターを用いて重みを再評価する。
新しいウエイト値で、上記の二乗和を最小化するプロセスを繰り返す。 収束するまでこの作業を続ける。 収束の基準は、現在のパラメータ値に対する重み付き残差の総和の平方根と、前の反復のパラメータ値に対する重み付き残差の総和の平方根との間の相対誤差が、式項目で設定された許容値より小さいことである。 他の推定方法と同様、収束は保証されない。
