Características generales
Novedades
En 2007, las funciones y características de SigmaStat se integraron en SigmaPlot a partir de la versión 11. Sin embargo, el 1 de febrero de 2016 se publicó SigmaStat 4.0, que ya está disponible como producto independiente.
A continuación se detallan las numerosas mejoras introducidas en las funciones de análisis estadístico de SigmaStat:
- Análisis de componentes principales (ACP) - El análisis de componentes principales es una técnica para reducir la complejidad de los datos de alta dimensión mediante la aproximación de los datos con menos dimensiones.
- Análisis de covarianza (ANCOVA) - El análisis de covarianza es una extensión del ANOVA (análisis de varianza) que se obtiene especificando una o más covariables como variables adicionales en el modelo.
- Regresión de Cox: incluye el modelo de riesgos proporcionales con estratificación para estudiar el impacto de los posibles factores de riesgo en el tiempo de supervivencia de una población. Los datos de entrada pueden ser categóricos.
- Prueba T de una muestra - Comprueba la hipótesis de que la media de una población es igual a un valor especificado.
- Pruebas de Odds Ratio y Riesgo Relativo - Ambas prueban la hipótesis de que un tratamiento no tiene efecto sobre la tasa de ocurrencia de algún evento específico en una población. La Odds Ratio se utiliza en estudios retrospectivos para determinar el efecto del tratamiento una vez observado el evento. El riesgo relativo se utiliza en estudios prospectivos en los que los grupos de tratamiento y control se han elegido antes de que se produzca el suceso.
- Prueba de normalidad de Shapiro-Wilk - Una prueba más precisa que la de Kolmogorov-Smirnov para evaluar la normalidad de los datos muestreados. Se utiliza en la comprobación de supuestos para muchas pruebas estadísticas, pero también se puede utilizar directamente en los datos de la hoja de cálculo.
- Nuevo Gráfico de Resultados - Gráficos de Perfil ANOVA: Se utiliza para analizar los efectos principales y las interacciones de orden superior de los factores en un diseño ANOVA multifactorial comparando las medias de los mínimos cuadrados.
- Nuevas transformadas de probabilidad - Se han añadido treinta y cuatro nuevas funciones al lenguaje de transformadas de SigmaStat para calcular probabilidades y puntuaciones asociadas a distribuciones que surgen en muchos campos de estudio.
- Nuevo cambio de interfaz - Regresión no lineal: Una interfaz de asistente fácil de usar e informes más detallados.
- Nuevo cambio en la interfaz: transformaciones rápidas: Una forma más sencilla de realizar cálculos en la hoja de cálculo.
- Nuevo cambio de interfaz - Nueva interfaz de usuario: Permite al usuario trabajar más fácilmente con hojas de cálculo de Excel.
- Corrección de Yates añadida a la prueba de Mann-Whitney - La corrección de Yates para la continuidad, o prueba chi-cuadrado de Yates, se utiliza cuando se comprueba la independencia en una tabla de contingencia al evaluar si dos muestras de observaciones proceden de la misma distribución.
- Mensajes de error mejorados - Los mensajes de error mejorados han añadido información cuando la comprobación de supuestos para ANOVA ha fallado.
- Regresión de Deming - La regresión de Deming tiene en cuenta los errores de las variables X e Y. Se trata de una técnica de comparación de métodos en la que los datos X proceden de un método y los datos Y del otro. El método de regresión Deming básicamente amplía la regresión lineal normal, en la que se considera que los valores X no tienen errores, al caso en que tanto X como Y (ambos métodos) tienen errores. A continuación, se pueden comprobar las hipótesis, la pendiente diferente de 1,0, por ejemplo, para determinar si los métodos son los mismos. Por ejemplo, podría utilizarse para comparar dos instrumentos diseñados para medir la misma sustancia o para comparar dos métodos algorítmicos de detección de tumores en imágenes. El gráfico compara los dos métodos para determinar si son diferentes o iguales. Un informe ofrece resultados estadísticos.
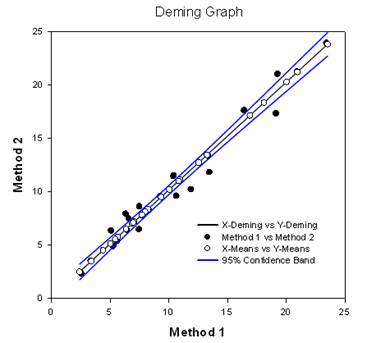
- Criterio de Información de Akaike (AICc) - El Criterio de Información de Akaike está ahora disponible en los informes de regresión no lineal. Se trata de un criterio de bondad de ajuste que también tiene en cuenta el número de parámetros de la ecuación. También es válido para ecuaciones no anidadas que se dan, por ejemplo, en análisis de cinética enzimática.
- Nuevas funciones de probabilidad para la regresión no lineal - Se han añadido un total de 24 funciones de probabilidad a la biblioteca de ajuste de curvas. Se han creado ecuaciones automáticas de estimación inicial de parámetros para cada una de ellas.
- Ponderación de regresión no lineal - Ahora hay siete funciones de ponderación diferentes incorporadas en cada ecuación de regresión no lineal (las 3D son ligeramente diferentes). Estas funciones son y recíproca, y recíproca al cuadrado, x recíproca, x recíproca al cuadrado, predicteds recíproca, predicteds recíproca al cuadrado y Cauchy. El algoritmo de mínimos cuadrados reponderados iterativamente se utiliza para permitir que las ponderaciones cambien durante cada iteración de regresión no lineal.
- Mejoras en las pruebas de comparación múltiple - Se han introducido dos mejoras importantes. Se han añadido los valores P para los resultados del ANOVA no paramétrico. Antes no existían. Además, los valores P de las comparaciones múltiples se limitaron a opciones discretas (0,05, 0,01, etc.). Esta limitación ya no existe y puede utilizarse cualquier valor P válido.
Nuevas pruebas estadísticas importantes
Análisis de componentes principales (ACP) – Elanálisis de componentes principales es una técnica para reducir la complejidad de los datos de alta dimensión mediante la aproximación de los datos con menos dimensiones. Cada nueva dimensión se denomina componente principal y representa una combinación lineal de las variables originales. El primer componente principal tiene en cuenta la mayor variación posible de los datos. Cada componente principal subsiguiente explica la mayor parte posible de la variación restante y es ortogonal a todos los componentes principales anteriores.
Puede examinar los componentes principales para comprender las fuentes de variación de sus datos. También puede utilizarlos para formar modelos predictivos. Si la mayor parte de la variación de los datos se encuentra en un subconjunto de baja dimensión, es posible que pueda modelizar la variable de respuesta en términos de componentes principales. Puede utilizar componentes principales para reducir el número de variables en regresión, agrupación y otras técnicas estadísticas. El objetivo principal del análisis de componentes principales es explicar las fuentes de variabilidad de los datos y representarlos con menos variables, conservando la mayor parte de la varianza total.
Ejemplos de gráficos de componentes principales:
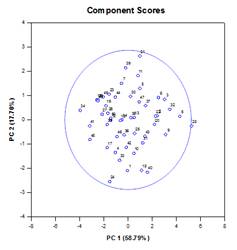
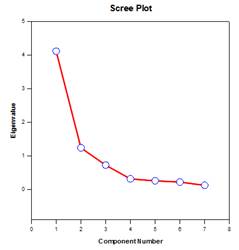
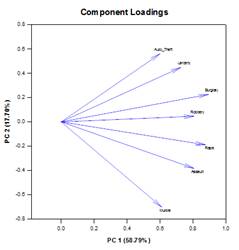
Análisisde co varianza (ANCOVA) – Elanálisis de covarianza es una extensión del ANOVA que se obtiene especificando una o más covariables como variables adicionales en el modelo. Si organiza los datos ANCOVA en una hoja de trabajo de SigmaPlot utilizando el formato de datos indexados, una columna representará el factor y una columna representará la variable dependiente (las observaciones) como en un diseño ANOVA. Además, tendrá una columna para cada covariable.
Ejemplos de gráficos ANCOVA:
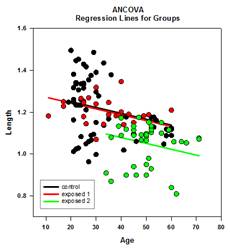
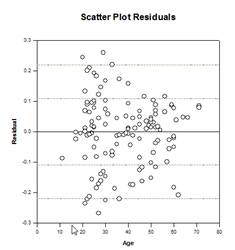
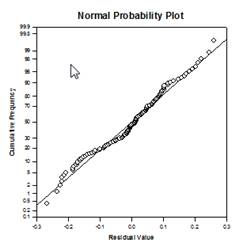
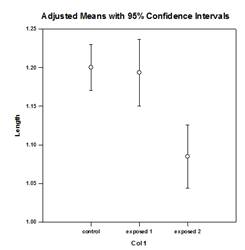
Nuevas funciones estadísticas
Mejoras en las comparaciones múltiples – Se ha realizado una mejora significativa en el cálculo del valor P de las comparaciones múltiples. Los siguientes procedimientos de comparación múltiple, Tukey (pruebas no paramétricas), SNK (pruebas no paramétricas), Dunnett’s, Dunn’s (sólo no paramétricas) y Duncan no calcularon los valores p analíticamente, sino que utilizaron tablas de consulta de valores críticos para una distribución concreta para determinar, mediante interpolación si era necesario, si una estadística de prueba calculada representaba una diferencia significativa en las medias de los grupos. Por lo tanto, no se comunicaron los valores p para estas pruebas, sino sólo la conclusión de si existía o no una diferencia significativa. Uno de los principales problemas de este enfoque es que las tablas de consulta sólo están disponibles para dos niveles de significación, 0,05 y 0,01. Otro problema es que muchos clientes quieren conocer los valores p. Para SigmaPlot, se han codificado algoritmos para calcular las distribuciones de los estadísticos de prueba para todos los procedimientos post-hoc, haciendo obsoletas las tablas de consulta. Como resultado, los p-valores ajustados para todos los procedimientos post-hoc se incluyen ahora en el informe. Además, ya no es necesario restringir el nivel de significación de las comparaciones múltiples a 0,05 o 0,01. En su lugar, el nivel de significación de las comparaciones múltiples será el mismo que el nivel de significación de la prueba principal (general). No hay ninguna limitación para este valor p: se puede utilizar cualquier valor válido.
Criterio de información de Akaike (AICc) – Se ha añadido el Criterio de información de Akaike a los informes del Asistente de regresión y del Asistente de ajuste dinámico y al cuadro de diálogo Opciones de informe. Proporciona un método para medir el rendimiento relativo en el ajuste de un modelo de regresión a un conjunto dado de datos. Basado en el concepto de entropía de la información, el criterio ofrece una medida relativa de la información que se pierde al utilizar un modelo para describir los datos.
Más concretamente, ofrece un compromiso entre maximizar la verosimilitud del modelo estimado (lo mismo que minimizar la suma de cuadrados residual si los datos se distribuyen normalmente) y mantener al mínimo el número de parámetros libres del modelo, reduciendo su complejidad. Aunque la bondad del ajuste casi siempre mejora añadiendo más parámetros, un ajuste excesivo aumentará la sensibilidad del modelo a los cambios en los datos de entrada y puede arruinar su capacidad de predicción.
La razón básica para utilizar el AIC es como guía para la selección de modelos. En la práctica, se calcula para un conjunto de modelos candidatos y un conjunto de datos determinado. El modelo con el valor AIC más bajo se selecciona como el modelo del conjunto que mejor representa el modelo «verdadero», o el modelo que minimiza la pérdida de información, que es lo que el AIC está diseñado para estimar.
Una vez determinado el modelo con el AIC mínimo, también se puede calcular una probabilidad relativa para cada uno de los otros modelos candidatos para medir la probabilidad de reducir la pérdida de información en relación con el modelo con el AIC mínimo. La probabilidad relativa puede ayudar al investigador a decidir si debe conservar más de un modelo del conjunto para seguir estudiándolo.
El cálculo del AIC se basa en la siguiente fórmula general obtenida por Akaike1
![]()
donde ![]() es el número de parámetros libres en el modelo y
es el número de parámetros libres en el modelo y ![]() es el valor maximizado de la función de verosimilitud para el modelo estimado.
es el valor maximizado de la función de verosimilitud para el modelo estimado.
Cuando el tamaño de la muestra de los datos ![]() es pequeño en relación con el número de parámetros
es pequeño en relación con el número de parámetros![]() (algunos autores dicen que cuando
(algunos autores dicen que cuando ![]() no es más que unas pocas veces mayor que
no es más que unas pocas veces mayor que ![]() ), el AIC no funcionará tan bien para proteger contra el sobreajuste. En este caso, existe una versión corregida del AIC dada por:
), el AIC no funcionará tan bien para proteger contra el sobreajuste. En este caso, existe una versión corregida del AIC dada por:
![]()
Se observa que el AICc impone una penalización mayor que el AIC cuando hay parámetros adicionales. La mayoría de los autores parecen estar de acuerdo en que debe utilizarse el AICc en lugar del AIC en todas las situaciones.
Funciones de ajuste probabilístico – Se han añadido 24 nuevas funciones de ajuste probabilístico a la biblioteca de ajuste standard.jfl. A continuación se muestran estas funciones y algunas ecuaciones y formas gráficas:

Como ejemplo, el archivo de ajuste para la función Densidad Lognormal contiene la ecuación para la densidad lognormal lognormden(x,a,b), ecuaciones para la estimación automática del parámetro inicial y las siete nuevas funciones de ponderación.
[Variables]
x = col(1)
y = col(2)
reciprocal_y = 1/abs(y)
recíproco_cuadrado = 1/y^2
recíproco_x = 1/abs(x)
recíproco_xcuadrado = 1/x^2
reciprocal_pred = 1/abs(f)
reciprocal_predsqr = 1/f^2
peso_Cauchy = 1/(1+4*(y-f)^2)
Funciones automáticas de estimación inicial de parámetros
trap(q,r)=.5*total(({0,q}+{q,0})[data(2,size(q))]*diff(r)[data(2,size(r))])
s=clasificar(complejo(x,y),x)
u = subbloque(s,1,1,1, tamaño(x))
v = subbloque(s,2,1,2, tamaño(y))
meanest = trap(u*v,u)
varest=trap((u-meanest)^2*v,u)
p = 1+varest/meanest^2
[Parameters]
a= if(media > 0, ln(media/cuadrado(p)), 0)
b= if(p >= 1, sqrt(ln(p)), 1)
[Equation]
f=lognormden(x,a,b)
ajustar f a y
» ajustar f a y con peso reciproco_y
«ajustar f a y con peso recíproco_cuadrado
«ajustar f a y con peso recíproco_x
«ajustar f a y con peso recíproco_xcuadrado
» ajustar f a y con peso reciprocal_pred
» ajustar f a y con peso reciprocal_predsqr
«ajustar f a y con peso peso_Cauchy
[Constraints]
b>0
[Options]
tolerancia=1e-010
stepize=1
iteraciones=200
Funciones de ponderación en regresión no lineal – SigmaPlot Los elementos de ecuación utilizan a veces una variable de ponderación con el fin de asignar un peso a cada observación (o respuesta) en un conjunto de datos de regresión. La ponderación de una observación mide su incertidumbre en relación con la distribución de probabilidad de la que se ha extraído. Una ponderación mayor indica una observación que varía poco de la media real de su distribución, mientras que una ponderación menor se refiere a una observación que se muestrea más de la cola de su distribución.
Según los supuestos estadísticos para estimar los parámetros de un modelo de ajuste utilizando el enfoque de mínimos cuadrados, las ponderaciones son, hasta un factor de escala, iguales al recíproco de las varianzas poblacionales de las distribuciones (gaussianas) de las que se muestrean las observaciones. En este caso, definimos un residuo, a veces denominado residuo bruto, como la diferencia entre una observación y el valor previsto (el valor del modelo ajustado) para un valor determinado de la(s) variable(s) independiente(s). Si las varianzas de las observaciones no son todas iguales(heteroscedasticidad), se necesita una variable de ponderación y se resuelve el problema de mínimos cuadrados ponderados de minimización de la suma ponderada de los cuadrados de los residuos para encontrar los parámetros de mejor ajuste.
Nuestra nueva función permitirá al usuario definir una variable de peso en función de los parámetros contenidos en el modelo de ajuste. Se han añadido siete funciones de peso predefinidas a cada función de ajuste (las funciones 3D son ligeramente diferentes). Los siete que se muestran a continuación son 1/y, 1/y2, 1/x, 1/x2, 1/predicho, 1/predicho2 y Cauchy.

Una aplicación de esta ponderación adaptativa más general es en situaciones en las que las varianzas de las observaciones no pueden determinarse antes de realizar el ajuste. Por ejemplo, si todas las observaciones tienen una distribución de Poisson, entonces las medias poblacionales, que son lo que están estimando los valores predichos, son iguales a las varianzas poblacionales. Aunque el método de los mínimos cuadrados para estimar los parámetros está diseñado para datos con distribución normal, a veces se utilizan otras distribuciones con mínimos cuadrados cuando no se dispone de otros métodos. En el caso de los datos de Poisson, tenemos que definir la variable de peso como el recíproco de los valores predichos. Este procedimiento se denomina a veces «ponderación por valores previstos».
Otra aplicación de la ponderación adaptativa es la obtención de procedimientos robustos para estimar parámetros que mitiguen los efectos de los valores atípicos. Ocasionalmente, puede haber unas pocas observaciones en un conjunto de datos que se muestrean a partir de la cola de sus distribuciones con una probabilidad pequeña, o hay unas pocas observaciones que se muestrean a partir de distribuciones que se desvían ligeramente del supuesto de normalidad utilizado en la estimación por mínimos cuadrados y, por lo tanto, contaminan el conjunto de datos. Estas observaciones aberrantes, llamadas valores atípicos en la variable de respuesta, pueden tener un impacto significativo en los resultados del ajuste porque tienen residuos relativamente grandes (brutos o ponderados) y, por lo tanto, inflan la suma de cuadrados que se está minimizando.
Una forma de mitigar los efectos de los valores atípicos es utilizar una variable de ponderación que sea una función de los residuos (y, por tanto, también una función de los parámetros), en la que la ponderación asignada a una observación esté inversamente relacionada con el tamaño del residuo. La definición de la función de ponderación depende de las suposiciones sobre las distribuciones de las observaciones (suponiendo que no sean normales) y de un esquema para decidir qué tamaño de residuo tolerar. La función de ponderación de Cauchy se define en términos de los residuos, y-f donde y es el valor de la variable dependiente y f es la función de ajuste, y puede utilizarse para minimizar el efecto de los valores atípicos.
peso_Cauchy = 1/(1+4*(y-f)^2)
El algoritmo de estimación de parámetros que utilizamos para la ponderación adaptativa, mínimos cuadrados reponderados iterativamente (IRLS), se basa en la resolución de una secuencia de problemas de mínimos cuadrados ponderados constantes en los que cada subproblema se resuelve utilizando nuestra implementación actual del algoritmo de Levenberg-Marquardt. Este proceso comienza con la evaluación de las ponderaciones utilizando los valores iniciales de los parámetros y, a continuación, minimizando la suma de cuadrados con estas ponderaciones fijas. A continuación, se utilizan los parámetros de mejor ajuste para reevaluar las ponderaciones.
Con los nuevos valores de peso, se repite el proceso anterior de minimización de la suma de cuadrados. Continuamos de este modo hasta alcanzar la convergencia. El criterio utilizado para la convergencia es que el error relativo entre la raíz cuadrada de la suma de los residuos ponderados para los valores actuales de los parámetros y la raíz cuadrada de la suma de los residuos ponderados para los valores de los parámetros de la iteración anterior sea inferior al valor de tolerancia establecido en el punto de la ecuación. Como ocurre con otros procedimientos de estimación, la convergencia no está garantizada.
