Analysis Features
New Features
In 2007, SigmaStat’s functions and features were integrated into SigmaPlot starting at version 11. However, on February 1, 2016, SigmaStat 4.0 was released and is now available as a standalone product.
Below are the many improvements to the statistical analysis functions in SigmaStat:
- Principal Components Analysis (PCA) – Principal component analysis is a technique for reducing the complexity of high-dimensional data by approximating the data with fewer dimensions.
- Analysis of Covariance (ANCOVA) – Analysis of Covariance is an extension of ANOVA (Analysis of Variance) obtained by specifying one or more covariates as additional variables in the model.
- Cox Regression – This includes the proportional hazards model with stratification to study the impact of potential risk factors on the survival time of a population. The input data can be categorical.
- One-Sample T-test – Tests the hypothesis that the mean of a population equals a specified value.
- Odds Ratio and Relative Risk tests – Both tests the hypothesis that a treatment has no effect on the rate of occurrence of some specified event in a population. Odds Ratio is used in retrospective studies to determine the treatment effect after the event has been observed. Relative Risk is used in prospective studies where the treatment and control groups have been chosen before the event occurs.
- Shapiro-Wilk Normality test – A more accurate test than Kolmogorov-Smirnov for assessing the normality of sampled data. Used in assumption checking for many statistical tests, but can also be used directly on worksheet data.
- New Result Graph – ANOVA Profile Plots: Used to analyze the main effects and higher-order interactions of factors in a multi-factor ANOVA design by comparing averages of the least square means.
- New Probability Transforms – Thirty four new functions have been added to SigmaStat’s Transform language for calculating probabilities and scores associated with distributions that arise in many fields of study.
- New Interface Change – Nonlinear Regression: An easy to use wizard interface and more detailed reports.
- New Interface Change – Quick Transforms: An easier way of performing computations in the worksheet.
- New Interface Change – New User Interface: Allows the user to work more easily with Excel worksheets.
- Yates correction added to the Mann-Whitney test – Yates correction for continuity, or Yates chi-square test is used when testing for independence in a contingency table when assessing whether two samples of observations come from the same distribution.
- Improved Error Messaging – Improved error messages have added information when assumption checking for ANOVA has failed.
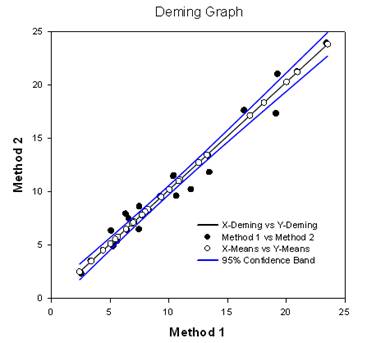
- Deming Regression – Deming regression allows for errors in both X and Y variables – a technique for method comparison where the X data is from one method and the y data the other. The Deming regression method basically extends the normal linear regression, where the X values are considered to be error-free, to the case where both X and Y (both methods) have error. Hypotheses can then be tested, slope different from 1.0 for example, to determine if the methods are the same. For example, it might be used to compare two instruments designed to measure the same substance or to compare two algorithmic methods of detecting tumors in images. The graph compares the two methods to determine if they are different or the same. A report gives statistical results.
- Akaike Information Criterion (AICc) – The Akaike Information Criterion is now available in nonlinear regression reports. It is a goodness of fit criterion that also accounts for the number of parameters in the equation. It also is valid for non-nested equations that occur, for example, in enzyme kinetics analyses.
- New Probability Functions for Nonlinear Regression – A total of 24 probability functions have been added to the curve fit library. Automatic initial parameter estimate equations have been created for each.
- Nonlinear Regression Weighting – There are now seven different weighting functions built into each nonlinear regression equation (3D are slightly different). These functions are reciprocal y, reciprocal y squared, reciprocal x, reciprocal x squared, reciprocal predicteds, reciprocal predicteds squared and Cauchy. The iteratively reweighted least squares algorithm is used to allow the weights to change during each nonlinear regression iteration.
- Multiple Comparison Test Improvements – Two important improvements have been made. P values for the results of nonparametric ANOVA have been added. These did not exist before. Also, multiple comparison P values were limited to discrete choices (0.05, 0.01, etc.). This limitation no longer exists and any valid P value may be used.
Major New Statistical Tests
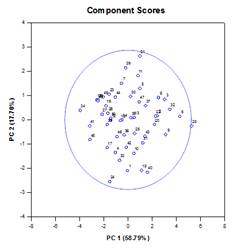
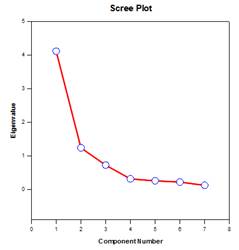
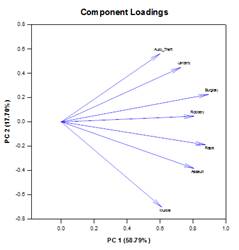
Principal Components Analysis (PCA) – Principal component analysis is a technique for reducing the complexity of high-dimensional data by approximating the data with fewer dimensions. Each new dimension is called a principal component and represents a linear combination of the original variables. The first principal component accounts for as much variation in the data as possible. Each subsequent principal component accounts for as much of the remaining variation as possible and is orthogonal to all of the previous principal components.
You can examine principal components to understand the sources of variation in your data. You can also use them in forming predictive models. If most of the variation in your data exists in a low-dimensional subset, you might be able to model your response variable in terms of the principal components. You can use principal components to reduce the number of variables in regression, clustering, and other statistical techniques. The primary goal of Principal Components Analysis is to explain the sources of variability in the data and to represent the data with fewer variables while preserving most of the total variance.
Examples of Principal Components Graphs:
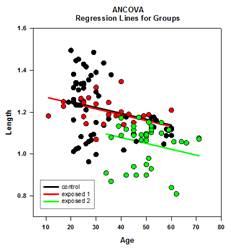
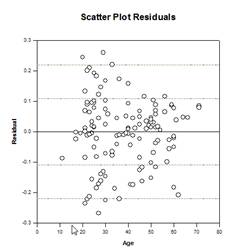
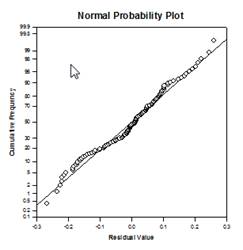
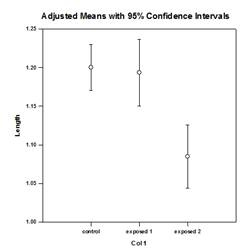
Analysis of Covariance (ANCOVA) – Analysis of Covariance is an extension of ANOVA obtained by specifying one or more covariates as additional variables in the model. If you arrange ANCOVA data in a SigmaPlot worksheet using the indexed data format, one column will represent the factor and one column will represent the dependent variable (the observations) as in an ANOVA design. In addition, you will have one column for each covariate.
Examples of ANCOVA Graphs:
New Statistical Features
 As an example, the fit file for the Lognormal Density function contains the equation for the lognormal density lognormden(x,a,b), equations for automatic initial parameter estimation and the seven new weighting functions.
[Variables]
x = col(1)
y = col(2)
reciprocal_y = 1/abs(y)
reciprocal_ysquare = 1/y^2
reciprocal_x = 1/abs(x)
reciprocal_xsquare = 1/x^2
reciprocal_pred = 1/abs(f)
reciprocal_predsqr = 1/f^2
weight_Cauchy = 1/(1+4*(y-f)^2)
‘Automatic Initial Parameter Estimate Functions
trap(q,r)=.5*total(({0,q}+{q,0})[data(2,size(q))]*diff(r)[data(2,size(r))])
s=sort(complex(x,y),x)
u = subblock(s,1,1,1, size(x))
v = subblock(s,2,1,2, size(y))
meanest = trap(u*v,u)
varest=trap((u-meanest)^2*v,u)
p = 1+varest/meanest^2
[Parameters]
a= if(meanest > 0, ln(meanest/sqrt(p)), 0)
b= if(p >= 1, sqrt(ln(p)), 1)
[Equation]
f=lognormden(x,a,b)
fit f to y
”fit f to y with weight reciprocal_y
”fit f to y with weight reciprocal_ysquare
”fit f to y with weight reciprocal_x
”fit f to y with weight reciprocal_xsquare
”fit f to y with weight reciprocal_pred
”fit f to y with weight reciprocal_predsqr
”fit f to y with weight weight_Cauchy
[Constraints]
b>0
[Options]
tolerance=1e-010
stepsize=1
iterations=200
Weight Functions in Nonlinear Regression – SigmaPlot equation items sometimes use a weight variable for the purpose of assigning a weight to each observation (or response) in a regression data set. The weight for an observation measures its uncertainty relative to the probability distribution from which it’s sampled. A larger weight indicates an observation which varies little from the true mean of its distribution while a smaller weight refers to an observation that is sampled more from the tail of its distribution.
Under the statistical assumptions for estimating the parameters of a fit model using the least squares approach, the weights are, up to a scale factor, equal to the reciprocal of the population variances of the (Gaussian) distributions from which the observations are sampled. Here, we define a residual, sometimes called a raw residual, to be the difference between an observation and the predicted value (the value of the fit model) at a given value of the independent variable(s). If the variances of the observations are not all the same (heteroscedasticity), then a weight variable is needed and the weighted least squaresproblem of minimizing the weighted sum of squares of the residuals is solved to find the best-fit parameters.
Our new feature will allow the user to define a weight variable as a function of the parameters contained in the fit model. Seven predefined weight functions have been added to each fit function (3D functions are slightly different). The seven shown below are 1/y, 1/y2, 1/x, 1/x2, 1/predicted, 1/predicteds2 and Cauchy.
As an example, the fit file for the Lognormal Density function contains the equation for the lognormal density lognormden(x,a,b), equations for automatic initial parameter estimation and the seven new weighting functions.
[Variables]
x = col(1)
y = col(2)
reciprocal_y = 1/abs(y)
reciprocal_ysquare = 1/y^2
reciprocal_x = 1/abs(x)
reciprocal_xsquare = 1/x^2
reciprocal_pred = 1/abs(f)
reciprocal_predsqr = 1/f^2
weight_Cauchy = 1/(1+4*(y-f)^2)
‘Automatic Initial Parameter Estimate Functions
trap(q,r)=.5*total(({0,q}+{q,0})[data(2,size(q))]*diff(r)[data(2,size(r))])
s=sort(complex(x,y),x)
u = subblock(s,1,1,1, size(x))
v = subblock(s,2,1,2, size(y))
meanest = trap(u*v,u)
varest=trap((u-meanest)^2*v,u)
p = 1+varest/meanest^2
[Parameters]
a= if(meanest > 0, ln(meanest/sqrt(p)), 0)
b= if(p >= 1, sqrt(ln(p)), 1)
[Equation]
f=lognormden(x,a,b)
fit f to y
”fit f to y with weight reciprocal_y
”fit f to y with weight reciprocal_ysquare
”fit f to y with weight reciprocal_x
”fit f to y with weight reciprocal_xsquare
”fit f to y with weight reciprocal_pred
”fit f to y with weight reciprocal_predsqr
”fit f to y with weight weight_Cauchy
[Constraints]
b>0
[Options]
tolerance=1e-010
stepsize=1
iterations=200
Weight Functions in Nonlinear Regression – SigmaPlot equation items sometimes use a weight variable for the purpose of assigning a weight to each observation (or response) in a regression data set. The weight for an observation measures its uncertainty relative to the probability distribution from which it’s sampled. A larger weight indicates an observation which varies little from the true mean of its distribution while a smaller weight refers to an observation that is sampled more from the tail of its distribution.
Under the statistical assumptions for estimating the parameters of a fit model using the least squares approach, the weights are, up to a scale factor, equal to the reciprocal of the population variances of the (Gaussian) distributions from which the observations are sampled. Here, we define a residual, sometimes called a raw residual, to be the difference between an observation and the predicted value (the value of the fit model) at a given value of the independent variable(s). If the variances of the observations are not all the same (heteroscedasticity), then a weight variable is needed and the weighted least squaresproblem of minimizing the weighted sum of squares of the residuals is solved to find the best-fit parameters.
Our new feature will allow the user to define a weight variable as a function of the parameters contained in the fit model. Seven predefined weight functions have been added to each fit function (3D functions are slightly different). The seven shown below are 1/y, 1/y2, 1/x, 1/x2, 1/predicted, 1/predicteds2 and Cauchy.
 One application of this more general adaptive weighting is in situations where the variances of the observations cannot be determined prior to performing the fit. For example, if all observations are Poisson distributed, then the population means, which are what the predicted values are estimating, equal to the population variances. Although the least squares approach for estimating parameters is designed for normally distributed data, other distributions are sometimes used with least squares when other methods are unavailable. In the case of Poisson data, we need to define the weight variable as the reciprocal of the predicted values. This procedure is sometimes referred to as “weighting by predicted values”.
Another application of adaptive weighting is to obtain robust procedures for estimating parameters that mitigate the effects of outliers. Occasionally, there may be a few observations in a data set that are sampled from the tail of their distributions with small probability, or there are a few observations that are sampled from distributions that deviate slightly from the normality assumption used in least squares estimation and thus contaminate the data set. These aberrant observations, called outliers in the response variable, can have a significant impact on the fit results because they have relatively large (raw or weighted) residuals and thus inflate the sum of squares that is being minimized.
One way to mitigate the effects of outliers is to use a weight variable that is a function of the residuals (and hence, also a function of the parameters), where the weight assigned to an observation is inversely related to the size of the residual. The definition of what weighting function to use depends upon assumptions about the distributions of observations (assuming they are not normal) and a scheme for deciding what size of residual to tolerate. The Cauchy weighting function is defined in terms of the residuals, y-f where y is the dependent variable value and f is the fitting function, and can be used for minimizing the effect of outliers.
weight_Cauchy = 1/(1+4*(y-f)^2)
The parameter estimation algorithm we use for adaptive weighting, iteratively reweighted least squares (IRLS), is based on solving a sequence of constant-weighted least squares problems where each sub-problem is solved using our current implementation of the Levenberg-Marquardt algorithm. This process begins by evaluating the weights using the initial parameter values and then minimizing the sum of squares with these fixed weights. The best-fit parameters are then used to re-evaluate the weights.
With the new weight values, the above process of minimizing the sum of squares is repeated. We continue in this fashion until convergence is achieved. The criterion used for convergence is that the relative error between the square root of the sum of the weighted residuals for the current parameter values and the square root of the sum of weighted residuals for the parameter values of the previous iteration is less than the tolerance value set in the equation item. As with other estimation procedures, convergence is not guaranteed.
One application of this more general adaptive weighting is in situations where the variances of the observations cannot be determined prior to performing the fit. For example, if all observations are Poisson distributed, then the population means, which are what the predicted values are estimating, equal to the population variances. Although the least squares approach for estimating parameters is designed for normally distributed data, other distributions are sometimes used with least squares when other methods are unavailable. In the case of Poisson data, we need to define the weight variable as the reciprocal of the predicted values. This procedure is sometimes referred to as “weighting by predicted values”.
Another application of adaptive weighting is to obtain robust procedures for estimating parameters that mitigate the effects of outliers. Occasionally, there may be a few observations in a data set that are sampled from the tail of their distributions with small probability, or there are a few observations that are sampled from distributions that deviate slightly from the normality assumption used in least squares estimation and thus contaminate the data set. These aberrant observations, called outliers in the response variable, can have a significant impact on the fit results because they have relatively large (raw or weighted) residuals and thus inflate the sum of squares that is being minimized.
One way to mitigate the effects of outliers is to use a weight variable that is a function of the residuals (and hence, also a function of the parameters), where the weight assigned to an observation is inversely related to the size of the residual. The definition of what weighting function to use depends upon assumptions about the distributions of observations (assuming they are not normal) and a scheme for deciding what size of residual to tolerate. The Cauchy weighting function is defined in terms of the residuals, y-f where y is the dependent variable value and f is the fitting function, and can be used for minimizing the effect of outliers.
weight_Cauchy = 1/(1+4*(y-f)^2)
The parameter estimation algorithm we use for adaptive weighting, iteratively reweighted least squares (IRLS), is based on solving a sequence of constant-weighted least squares problems where each sub-problem is solved using our current implementation of the Levenberg-Marquardt algorithm. This process begins by evaluating the weights using the initial parameter values and then minimizing the sum of squares with these fixed weights. The best-fit parameters are then used to re-evaluate the weights.
With the new weight values, the above process of minimizing the sum of squares is repeated. We continue in this fashion until convergence is achieved. The criterion used for convergence is that the relative error between the square root of the sum of the weighted residuals for the current parameter values and the square root of the sum of weighted residuals for the parameter values of the previous iteration is less than the tolerance value set in the equation item. As with other estimation procedures, convergence is not guaranteed. 