SigmaPlot Produkteigenschaften
Funktionen und Verbesserungen in SigmaPlot
- Waldgrundstücke
- Kerndichtediagramme
- 10 neue Farbschemata
- Punktdichtediagramm mit Mittelwert und Standardfehlerbalken
- Legende Verbesserungen
- Horizontale, vertikale und rechteckige Legendenformen
- Cursor über Seite oder oberen oder unteren Griff

-
- ermöglicht mehrspaltige Legenden
-
- Benutzeroberfläche zum Einstellen der Anzahl der Spalten für Legendenelemente im Dialogfeld Eigenschaften. Die zulässigen Spaltennummern werden in der Kombinationsliste angezeigt
- Ändern Sie die Anzahl der Spalten für die Legende, indem Sie den mittleren Griff im Begrenzungsrahmen auswählen und ziehen.
- Legendenelemente neu ordnen
- Über den Eigenschaftsdialog – Verschieben Sie ein oder mehrere Legendenelemente nach oben oder unten, indem Sie die Aufwärts-/Abwärts-Steuerung oben im Listenfeld verwenden.
- Durch Bewegen des Cursors – ein oder mehrere Legendenelemente nach oben oder unten verschieben. Wählen Sie das/die Legendenelement(e) und verwenden Sie die Pfeiltasten der Tastatur, um sich innerhalb des Begrenzungsrahmens zu bewegen.
- Durch Mausauswahl und Cursorbewegung für Elemente im Begrenzungsrahmen
- Eigenschaftseinstellungen für einzelne Legendenelemente – wählen Sie einzelne Legendenelemente aus und verwenden Sie die Mini-Symbolleiste, um die Eigenschaften zu ändern
- Legende Box leeren Bereich Kontrolle durch Cursor
- Cursor über Eckgriff


- ermöglicht eine proportionale Größenänderung
- Einfache Direktbeschriftung hinzufügen
- Unterstützung von “Direct Labeling” im Eigenschaftsdialog über das Kontrollkästchen “Direct Labeling”.
- Gruppierung der Legendenelemente aufheben – die einzelnen Legendenelemente können an die gewünschte Stelle verschoben werden und sich zusammen mit dem Diagramm bewegen
- Die Unterstützung für Legendentitel wurde hinzugefügt (standardmäßig kein Titel). Der Benutzer kann dem Legendenfeld einen Titel hinzufügen, indem er das Legenden-Eigenschaftsfeld verwendet
- Umkehrung der Legendenelemente über das Rechtsklick-Kontextmenü
- Öffnen Sie die Legendeneigenschaften, indem Sie entweder auf Legende Vollton oder Legende Text doppelklicken.
- Zurücksetzen wurde zu Legenden hinzugefügt, um die Legendenoptionen auf die Standardwerte zurückzusetzen.
- Horizontale, vertikale und rechteckige Legendenformen
Analysefunktionen
- Hauptkomponentenanalyse (PCA)
- Analyse der Kovarianz (ANCOVA)
- P-Werte zu Mehrfachvergleichen für nicht-parametrische ANOVAs hinzugefügt
- Die Auswahlmöglichkeiten für die Signifikanzniveaus von Mehrfachvergleichen wurden entfernt und das Signifikanzniveau von Mehrfachvergleichen an den Haupttest (Omnibus) gebunden.
- Hinzufügen des Akaike-Informationskriteriums zu den Berichten des Regressionsassistenten und des Assistenten für dynamische Anpassung sowie zum Dialogfeld “Berichtsoptionen
- Die Schaltfläche Rerun in der SigmaStat-Gruppe wurde wieder hinzugefügt.
- Aktualisierte die Anpassungsbibliothek standard.jfl
- Hinzufügen von 24 Wahrscheinlichkeitsfunktionen für die Kurvenanpassung oder Funktionsvisualisierung.
- Der Toleranzwert für alle Gleichungen wurde dahingehend geändert, dass nun die “e-Notation” anstelle einer festen Dezimalzahl verwendet wird. So kann der Benutzer den Wert ohne Scrollen lesen.
- Hinzufügen von sieben Gewichtungsfunktionen zu allen Kurvenanpassungsgleichungen in standard.jfl. Für 3D-Gleichungen gibt es eine leichte Variante.
Funktionen der Benutzeroberfläche
- Neuanordnung von Notizbucheinträgen in einem Abschnitt durch Ziehen
- SigmaPlot Tutorial PDF-Datei
- Linienbreiten aus einer Arbeitsblattspalte
Funktionen zum Importieren/Exportieren
- Hinzufügen der Dateiformate SVG und SWF für den Export skalierbarer Vektorgrafiken
- Vektor-PDF-Export hinzugefügt, um das bestehende Raster-PDF zu verbessern
- Unterstützung für den Import und Export von Dateien für die Versionen 13 und 14 von Minitab, Version 9 von SAS, Version 19 von SPSS und Version 13 von Symphony
SigmaPlot Produkteigenschaften
Waldgrundstück
Ein Walddiagramm ist eine Form der "Meta-Analyse", die dazu dient, mehrere Analysen zur gleichen Fragestellung zu kombinieren. Bei der Metaanalyse werden die Stichproben der einzelnen beitragenden Studien statistisch kombiniert, um eine zusammenfassende Gesamtstatistik zu erstellen, die präziser ist als die Effektgröße in den einzelnen Studien. Einzelne Studienwerte und ihre 95%-Konfidenzintervalle werden als quadratische Symbole mit horizontalen Fehlerbalken dargestellt, die zusammenfassende Gesamtstatistik als Raute mit einer Breite, die dem 95%-Konfidenzintervall entspricht.

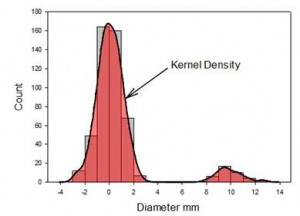
Kernel-Dichte
Die Kernel-Dichte-Funktion erzeugt eine Schätzung der zugrunde liegenden Datenverteilung. Dies sollte mit dem stufenförmigen Histogramm verglichen werden. Es hat Vorteile (keine Balken) und Nachteile (Verlust von Zählinformationen) gegenüber einem Histogramm und sollte in Verbindung mit dem Histogramm verwendet werden. Sie können gleichzeitig erstellt werden.
Punktdichte mit Mittelwert und Standardfehlerbalken
Die Berechnung von Mittelwert plus Standardfehlerbalken, Symbol plus Fehlerbalken, wurde dem Punktdichte-Diagramm hinzugefügt. Dadurch werden die anderen möglichen Punktdichte-Anzeigestatistiken - Mittelwert, Median, Perzentile und Boxplot - verbessert.

Farbschemata
Es wurden zehn neue Farbschemata eingeführt. Im Folgenden werden drei Beispiele aufgeführt:
Legendenverbesserungen - Gestalten
Es sind jetzt vertikale, horizontale und rechteckige Legendenformen verfügbar.
Umgekehrte Reihenfolge der Legende
Sie können nun auswählen, dass die Reihenfolge der Legendenelemente umgekehrt wird. Dies bietet eine logischere Reihenfolge für einige Diagrammtypen.
Legendenartikel neu bestellen
Es gibt drei Möglichkeiten, die Legendenelemente neu anzuordnen. Wie hier gezeigt, können Sie ein oder mehrere Legendenelemente nach oben oder unten verschieben, indem Sie die Aufwärts-/Abwärtspfeile im Legendenbedienfeld der Diagrammeigenschaften verwenden. Noch einfacher ist es, wenn Sie das Element in der Legende auswählen und die Pfeiltasten der Tastatur nach oben und unten verwenden. Oder Sie markieren das Legendenelement und ziehen es mit dem Mauszeiger an die neue Position.
Mini-Symbolleiste zur Bearbeitung von Legendenelementen
Legendenelemente können nun bearbeitet werden, indem Sie auf das Element klicken und die Mini-Symbolleiste verwenden.

Direkte Beschriftung
Die Gruppierung der Legende kann nun aufgehoben und einzelne Legendenelemente können neben den entsprechenden Plots platziert werden. Die Beschriftungen bewegen sich mit dem Diagramm, um ihre Position in Bezug auf das Diagramm beizubehalten. Da die Beschriftung neben der Fläche angebracht ist, ist die visuelle Identifizierung der einzelnen Flächen nun viel einfacher.
Hauptkomponentenanalyse (PCA)

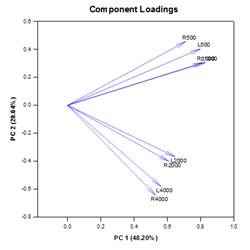
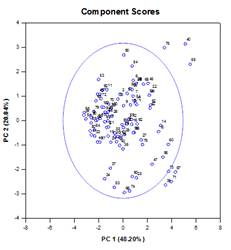
Die Hauptkomponentenanalyse (PCA) ist eine Technik zur Verringerung der Komplexität hochdimensionaler Daten durch Annäherung der Daten mit weniger Dimensionen. Jede neue Dimension wird als Hauptkomponente bezeichnet und stellt eine lineare Kombination der ursprünglichen Variablen dar. Die erste Hauptkomponente berücksichtigt so viel Variation in den Daten wie möglich. Jede nachfolgende Hauptkomponente berücksichtigt so viel der verbleibenden Variation wie möglich und ist orthogonal zu allen vorherigen Hauptkomponenten.
Sie können Hauptkomponenten untersuchen, um die Quellen der Variation in Ihren Daten zu verstehen. Sie können sie auch zur Erstellung von Vorhersagemodellen verwenden. Wenn der größte Teil der Variation in Ihren Daten in einer niedrigdimensionalen Teilmenge vorliegt, können Sie Ihre Antwortvariable möglicherweise anhand der Hauptkomponenten modellieren. Sie können Hauptkomponenten verwenden, um die Anzahl der Variablen bei Regression, Clustering und anderen statistischen Verfahren zu reduzieren.
Sie können Hauptkomponenten untersuchen, um die Quellen der Variation in Ihren Daten zu verstehen. Sie können sie auch zur Erstellung von Vorhersagemodellen verwenden. Wenn der größte Teil der Variation in Ihren Daten in einer niedrigdimensionalen Teilmenge vorliegt, können Sie Ihre Antwortvariable möglicherweise anhand der Hauptkomponenten modellieren. Sie können Hauptkomponenten verwenden, um die Anzahl der Variablen bei Regression, Clustering und anderen statistischen Verfahren zu reduzieren.
Die grafische Ausgabe besteht aus Scree-, Component Loadings- und Component Scores-Diagrammen.
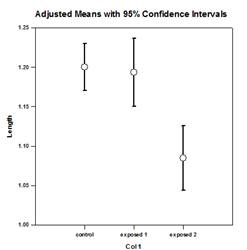
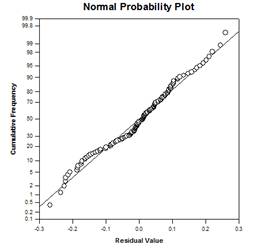
Analyse der Kovarianz (ANCOVA)
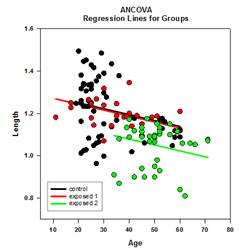
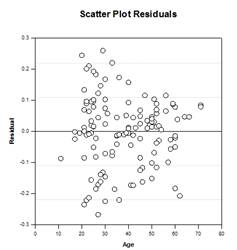
Ein Ein-Faktor-ANOVA-Modell basiert auf einem vollständig randomisierten Design, bei dem die Probanden einer Studie nach dem Zufallsprinzip aus einer Grundgesamtheit gezogen werden und dann jeder Proband nach dem Zufallsprinzip einer von mehreren Faktorstufen oder Behandlungen zugewiesen wird, so dass jeder Proband die gleiche Wahrscheinlichkeit hat, eine Behandlung zu erhalten. Eine gängige Annahme bei diesem Design ist, dass die Probanden homogen sind. Das bedeutet, dass jede andere Variable, bei der Unterschiede zwischen den Probanden bestehen, den Behandlungseffekt nicht signifikant verändert und nicht in das Modell aufgenommen werden muss. Allerdings gibt es häufig Variablen, die sich der Kontrolle des Untersuchers entziehen und die Beobachtungen innerhalb einer oder mehrerer Faktorgruppen beeinflussen, was zu notwendigen Anpassungen der Gruppenmittelwerte, ihrer Fehler, der Quellen der Variabilität und der P-Werte des Gruppeneffekts, einschließlich multipler Vergleiche, führt.
Diese Variablen werden als Kovariaten bezeichnet. Sie sind in der Regel kontinuierliche Variablen, können aber auch kategorisch sein. Da sie in der Regel von untergeordneter Bedeutung für die Studie sind und, wie oben erwähnt, vom Untersucher nicht kontrolliert werden können, stellen sie keine zusätzlichen Haupteffektfaktoren dar, können aber dennoch in das Modell aufgenommen werden, um die Genauigkeit der Ergebnisse zu verbessern. Kovariaten werden auch als Störvariablen oder Begleitvariablen bezeichnet.
ANCOVA (Analysis of Covariance) ist eine Erweiterung der ANOVA, bei der eine oder mehrere Kovariaten als zusätzliche Variablen in das Modell aufgenommen werden. Wenn Sie ANCOVA-Daten in einem SigmaPlot-Arbeitsblatt unter Verwendung des indizierten Datenformats anordnen, steht eine Spalte für den Faktor und eine Spalte für die abhängige Variable (die Beobachtungen), wie in einem ANOVA-Design. Außerdem haben Sie eine Spalte für jede Kovariate. Bei Verwendung eines Modells, das die Auswirkungen von Kovariaten einbezieht, wird eine größere Variabilität des Wertes der abhängigen Variable erklärt.
Dies verringert im Allgemeinen die unerklärte Varianz, die auf die zufällige Stichprobenvariabilität zurückzuführen ist, was die Sensitivität der ANCOVA im Vergleich zum gleichen Modell ohne Kovariaten (ANOVA-Modell) erhöht. Eine höhere Testsensitivität bedeutet, dass kleinere Mittelwertunterschiede zwischen den Behandlungen im Vergleich zu einem ANOVA-Standardmodell signifikant werden, wodurch die statistische Aussagekraft erhöht wird.
Ein einfaches Beispiel für die Verwendung von ANCOVA ist ein Experiment, bei dem die Schüler nach dem Zufallsprinzip einer von drei Unterrichtsmethoden zugewiesen werden und ihre Leistungen gemessen werden. Ziel ist es, die Wirkung der verschiedenen Methoden zu messen und festzustellen, ob eine Methode eine deutlich höhere Durchschnittspunktzahl als die anderen erreicht. Die Methoden sind Vortrag, Selbststudium und kooperatives Lernen. Die Durchführung einer Einweg-ANOVA für diese hypothetischen Daten ergibt die Ergebnisse in der nachstehenden Tabelle unter der Spaltenüberschrift ANOVA. Wir kommen zu dem Schluss, dass es keinen signifikanten Unterschied zwischen den Unterrichtsmethoden gibt. Es ist auch zu beachten, dass die durch das ANOVA-Modell nicht erklärte Varianz, die auf die Stichprobenvariabilität in den Beobachtungen zurückzuführen ist, auf 35,17 geschätzt wird.
Es ist möglich, dass die Schüler in unserer Studie aufgrund ihrer bisherigen schulischen Leistungen mehr von einer Methode profitieren als von den anderen. Nehmen wir an, wir verfeinern die Studie, um eine Kovariate einzubeziehen, die eine frühere Fähigkeit misst, z. B. ein staatlich anerkanntes standardbasiertes Assessment (SBA). Die Durchführung einer einseitigen ANCOVA mit diesen Daten führt zu den Ergebnissen in der nachstehenden Tabelle unter der Spaltenüberschrift ANCOVA.
Der bereinigte Mittelwert, der in der Tabelle für jede Methode angegeben ist, ist eine Korrektur des Gruppenmittelwerts zur Kontrolle der Auswirkungen der Kovariate. Die Ergebnisse zeigen, dass die bereinigten Mittelwerte signifikant unterschiedlich sind, wobei die Vorlesungsmethode die erfolgreichere ist. Beachten Sie, dass die Standardfehler der Mittelwerte fast um den Faktor drei abgenommen haben, während die Varianz aufgrund der Stichprobenvariabilität um den Faktor zehn abgenommen hat. Eine Verringerung des Fehlers ist die übliche Folge der Einführung von Kovariaten und der Durchführung einer ANCOVA-Analyse.
Es gibt vier ANCOVA-Ergebnisdiagramme - Regressionslinien in Gruppen, Streudiagramm der Residuen, angepasste Mittelwerte mit Konfidenzintervallen und Normalitätswahrscheinlichkeitsdiagramm:
P-Werte für nichtparametrische ANOVAs
Die nicht-parametrischen ANOVA-Tests in SigmaPlot sind der Kruskal-Wallis-Test (einfaktorielle ANOVA über Ränge) und der Friedman-Test (einfaktorielle ANOVA über Ränge mit wiederholten Maßnahmen). Beide bieten vier Post-hoc-Testverfahren, um die Quelle signifikanter Effekte im Behandlungsfaktor zu bestimmen. Die vier Verfahren sind Tukey, SNK, Dunn's und Dunnett's.
Die ersten drei Verfahren können verwendet werden, um die Signifikanz jedes paarweisen Vergleichs der Behandlungsgruppen zu testen, während die letzten beiden Verfahren verwendet werden können, um die Signifikanz von Vergleichen mit einer Kontrollgruppe zu testen. Die Dunn-Methode ist das einzige Verfahren, das zur Verfügung steht, wenn die Behandlungsgruppen ungleiche Stichprobengrößen haben.
Wenn ein Post-hoc-Testverfahren verwendet wird, enthält der Bericht eine Tabelle mit den Ergebnissen für die paarweisen Vergleiche der Behandlungsstufen. Die letzte Spalte der Tabelle zeigt, ob der Unterschied in den Rängen signifikant ist oder nicht. In früheren Versionen von SigmaPlot wird kein angepasster p-Wert angegeben, der mit dem Signifikanzniveau der ANOVA (normalerweise .05) verglichen werden kann, um die Signifikanz zu bestimmen.
Dies liegt daran, dass SigmaPlot die Signifikanz durch den Vergleich der beobachteten Teststatistik, die für jeden Vergleich berechnet wird, mit einem kritischen Wert der Verteilung der Statistik, der aus einer Nachschlagetabelle erhalten wird, bestimmt. SigmaPlot verfügte über zwei Sätze von Nachschlagetabellen für die Wahrscheinlichkeitsverteilungen, die den vier Post-hoc-Methoden entsprachen, wobei ein Satz für ein Signifikanzniveau von 0,05 und ein weiterer Satz für ein Signifikanzniveau von 0,01 galt.
Dies wurde kürzlich geändert, um analytische Verfahren zur Berechnung der p-Werte dieser Verteilungen zu verwenden, wodurch die Nachschlagetabellen überflüssig wurden. Aufgrund dieser Änderung sind wir nun in der Lage, die bereinigten p-Werte für jeden paarweisen Vergleich anzugeben. Diese Änderung ermöglicht es auch, die Einschränkung aufzuheben, dass .05 und .01 die einzigen Signifikanzniveaus für Mehrfachvergleiche sind. Der Benutzer kann also ein beliebiges gültiges Signifikanzniveau von 0 bis 1 für den P-Wert eingeben.
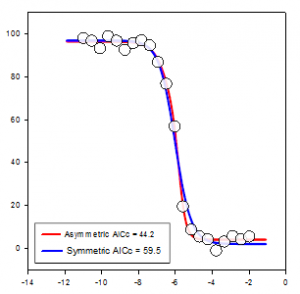
Akaike-Informationskriterium (AICc)
Das Akaike-Informationskriterium (AIC) ist eine Methode zur Messung der relativen Leistung bei der Anpassung eines Regressionsmodells an einen bestimmten Datensatz. Das Kriterium basiert auf dem Konzept der Informationsentropie und bietet ein relatives Maß für den Informationsverlust bei der Verwendung eines Modells zur Beschreibung der Daten. Genauer gesagt ist es ein Kompromiss zwischen der Maximierung der Wahrscheinlichkeit für das geschätzte Modell (das entspricht der Minimierung der Summe der Residuenquadrate, wenn die Daten normalverteilt sind) und der Minimierung der Anzahl der freien Parameter im Modell, wodurch dessen Komplexität reduziert wird. Obwohl die Anpassungsgüte fast immer durch das Hinzufügen weiterer Parameter verbessert wird, erhöht sich durch eine Überanpassung die Empfindlichkeit des Modells gegenüber Änderungen der Eingabedaten und kann seine Vorhersagefähigkeit beeinträchtigen.
Der Hauptgrund für die Verwendung von AIC ist die Orientierung bei der Modellauswahl. In der Praxis wird sie für eine Reihe von Modellkandidaten und einen bestimmten Datensatz berechnet. Das Modell mit dem kleinsten AIC-Wert wird als das Modell in der Menge ausgewählt, das das "wahre" Modell am besten repräsentiert, oder das Modell, das den Informationsverlust minimiert, was das Ziel der AIC-Schätzung ist. Nachdem das Modell mit dem minimalen AIC ermittelt wurde, kann auch eine relative Wahrscheinlichkeit für jedes der anderen in Frage kommenden Modelle berechnet werden, um die Wahrscheinlichkeit der Verringerung des Informationsverlusts im Vergleich zum Modell mit dem minimalen AIC zu messen. Die relative Wahrscheinlichkeit kann dem Untersucher bei der Entscheidung helfen, ob mehr als ein Modell in der Menge für die weitere Betrachtung beibehalten werden sollte.
Die Berechnung des AIC basiert auf der folgenden, von Akaike aufgestellten allgemeinen Formel
Es zeigt sich, dass AICc einen größeren Nachteil als AIC auferlegt, wenn es zusätzliche Parameter gibt. Die meisten Autoren scheinen darin übereinzustimmen, dass AICc in allen Situationen anstelle von AIC verwendet werden sollte, und es ist AICc, das in SigmaPlot implementiert ist. Die asymmetrische Gleichung in der Grafik ist deutlich besser als die symmetrische, da ihr AICc-Wert um mehr als 7 Einheiten niedriger ist als der der symmetrischen Gleichung - eine Faustregel für AICc. Wenn die Differenz größer als 2 ist, sollte die Gleichung mit dem kleineren AICc-Wert nicht als beste Gleichung, sondern eher als Kandidat für die beste Gleichung betrachtet werden.
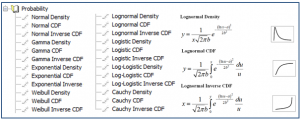
Nichtlineare Regressionswahrscheinlichkeitsfunktionen
Der Fit-Bibliothek standard.jfl wurden 24 neue Wahrscheinlichkeits-Fit-Funktionen hinzugefügt. Diese Funktionen sowie einige Gleichungen und Diagrammformen sind unten dargestellt.
Nichtlineare Regressionsgewichtungsfunktionen
Es gibt jetzt sieben verschiedene Gewichtungsfunktionen, die in jede nichtlineare Regressionsgleichung eingebaut sind (3D ist leicht unterschiedlich). Diese Funktionen sind reziprok y, reziprok y zum Quadrat, reziprok x, reziprok x zum Quadrat, reziprok predicteds, reziprok predicteds zum Quadrat und Cauchy. Der Algorithmus der iterativ neu gewichteten kleinsten Quadrate wird verwendet, damit sich die Gewichte während jeder Iteration der nichtlinearen Regression ändern können. Auf diese Weise kann die "Gewichtung nach Prädikaten", eine häufig verwendete Methode, durch Auswahl der Option reciprocal_pred weighting erreicht werden.

Außerdem kann die Cauchy-Gewichtung (wählen Sie weight_Cauchy) verwendet werden, um eine Gleichung an Daten anzupassen, die Ausreißer enthalten, und die Auswirkungen der Ausreißer werden minimiert. Benutzer können ihre eigenen Gewichtungsmethoden in Bezug auf Residuen und/oder Parameter erstellen, um andere robuste Anpassungsmethoden zu implementieren. Der Gleichungsteil einer Fit-Datei wird mit den sieben eingebauten Gewichtungsfunktionen dargestellt.
Funktionen der Benutzeroberfläche - Ordnen Sie Elemente in Ihrem Notizbuch durch Ziehen neu an.
Die Objekte in einem Notizbuchabschnitt werden nicht unbedingt in einer logischen Reihenfolge erstellt. Sie können nun Elemente innerhalb eines Abschnitts an neue Positionen ziehen, um sie logischer zu platzieren.
Ein aktualisiertes SigmaPlot Tutorial
Das neue Tutorial macht das erstmalige Erstellen von Diagrammen leicht. Es beginnt mit einfachen Beispielen und wird nach und nach komplexer.
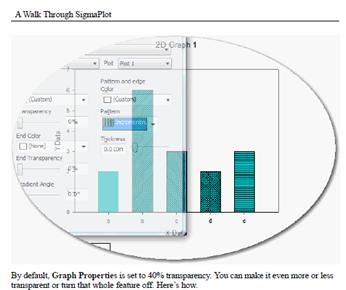

Angeben von Plotlinienbreiten aus einer Arbeitsblattspalte
Linienbreitenwerte können jetzt in eine Arbeitsblattspalte eingegeben werden. Diese Werte können innerhalb eines Diagramms oder für mehrere Diagramme auf der Seite verwendet werden.
Vektor-Export-Dateiformate
Die Dateiformate SVG (Scalable Vector Graphics), SWF (Adobe Flash Player) und Vector PDF wurden hinzugefügt. Dabei handelt es sich um skalierbare Formate, bei denen die Auflösung beim Zoomen auf verschiedene Ebenen nicht verloren geht. SVG ist das Standard-Grafikformat für das Web und SWF kann mit dem Adobe Flash Player verwendet werden. Da PDF so häufig verwendet wird, ist das Vektor-PDF-Format jetzt an die Schaltfläche PDF erstellen im Menüband Start angehängt.
Aktualisierte Formate für Antragsdateien
Die Unterstützung für den Import und Export von Dateien wurde auf die Versionen 13 und 14 von Minitab, Version 9 von SAS und Version 19 von SPSS aktualisiert.
