الميزات والتحسينات في SigmaPlot
- مؤامرات الغابات
- مؤامرات كثافة النواة
- 10 أنظمة ألوان جديدة
- الرسم البياني للكثافة النقطية مع أشرطة الخطأ المتوسطة والمعيارية
- تحسينات الأسطورة
- الأشكال الأسطورية الأفقية والرأسية والمستطيلة
- المؤشر على الجانب أو المقبض العلوي أو السفلي

-
- يسمح بأساطير متعددة الأعمدة
-
- واجهة المستخدم لتعيين عدد أعمدة عناصر وسيلة الإيضاح في مربع حوار الخصائص. يتم عرض أرقام الأعمدة المسموح بها في قائمة التحرير والسرد
- قم بتغيير عدد أعمدة عناصر وسيلة الإيضاح عن طريق تحديد وسحب المقبض الأوسط في المربع المحيط
- إعادة ترتيب العناصر وسيلة الإيضاح
- من خلال مربع حوار الخصائص – قم بتحريك عنصر واحد أو عدة عناصر إيضاحية لأعلى أو لأسفل باستخدام عنصر التحكم لأعلى/لأسفل الموجود أعلى مربع القائمة
- من خلال حركة المؤشر – حرك عنصرًا واحدًا أو أكثر من عناصر وسيلة الإيضاح لأعلى أو لأسفل. حدد عنصر (عناصر) وسيلة الإيضاح واستخدم مفتاح السهم لأعلى ولأسفل بلوحة المفاتيح للتنقل داخل المربع المحيط
- من خلال تحديد الماوس وحركة المؤشر للعناصر الموجودة في المربع المحيط
- إعدادات خصائص عناصر وسيلة الإيضاح الفردية – حدد عناصر وسيلة الإيضاح الفردية واستخدم شريط الأدوات المصغر لتغيير الخصائص
- التحكم في المنطقة الفارغة في مربع وسيلة الإيضاح من خلال المؤشر
- المؤشر فوق مقبض الزاوية


- يسمح بتغيير الحجم النسبي
- أضف علامات مباشرة بسيطة
- دعم “التسمية المباشرة” في مربع حوار الخصائص باستخدام عنصر التحكم في مربع الاختيار “التسمية المباشرة”
- فك تجميع عناصر وسيلة الإيضاح – يمكن نقل عناصر وسيلة الإيضاح الفردية إلى المواقع المفضلة ونقلها جنبًا إلى جنب مع الرسم البياني
- تمت إضافة دعم عنوان وسيلة الإيضاح (لا يوجد عنوان بشكل افتراضي). يمكن للمستخدم إضافة عنوان إلى مربع وسيلة الإيضاح باستخدام لوحة خصائص وسيلة الإيضاح
- قم بعكس عناصر وسيلة الإيضاح باستخدام قائمة سياق النقر بزر الماوس الأيمن
- افتح خصائص وسيلة الإيضاح بالنقر المزدوج فوق Legend Solid أو Legend Text
- تمت إضافة إعادة التعيين إلى وسائل الإيضاح لإعادة تعيين خيارات وسيلة الإيضاح إلى الوضع الافتراضي
- الأشكال الأسطورية الأفقية والرأسية والمستطيلة
ميزات التحليل
- تحليل المكونات الرئيسية (PCA)
- تحليل التباين (ANCOVA)
- تمت إضافة قيم P إلى مقارنات متعددة لـ ANOVAs غير المعلمية
- تمت إزالة اختيارات مربع التحرير والسرد للمستويات الهامة للمقارنة المتعددة وربط مستوى أهمية المقارنات المتعددة بالاختبار الرئيسي (الجامع)
- تمت إضافة معيار معلومات Akaike إلى تقارير معالج الانحدار ومعالج التناسب الديناميكي ومربع حوار خيارات التقرير
- تمت إضافة زر إعادة التشغيل مرة أخرى في مجموعة SigmaStat
- تم تحديث المكتبة الملائمة Standard.jfl
- تمت إضافة وظائف الاحتمال، لتشمل الآن 24، لتركيب المنحنى أو تصور الوظيفة
- تم تعديل قيمة التسامح لجميع المعادلات لاستخدام “التدوين الإلكتروني” بدلاً من العلامة العشرية الثابتة. وهذا يسمح للمستخدم بقراءة القيمة دون التمرير.
- أضف سبع وظائف ترجيح إلى جميع معادلات تناسب المنحنى في Standard.jfl. هناك متغير طفيف مضاف للمعادلات ثلاثية الأبعاد.
ميزات واجهة المستخدم
- إعادة ترتيب عناصر دفتر الملاحظات في قسم عن طريق السحب
- ملف PDF تعليمي SigmaPlot التعليمي
- عرض الخط من عمود ورقة العمل
ميزات الاستيراد/التصدير
- تمت إضافة تنسيقات الملفات SVG وSWF لتصدير الرسومات المتجهة القابلة للتطوير
- تمت إضافة تصدير Vector PDF لتحسين ملف PDF النقطي الموجود
- تمت إضافة دعم استيراد وتصدير الملفات للإصدارين 13 و14 من Minitab، والإصدار 9 من SAS، والإصدار 19 من SPSS، والإصدار 13 من Symphony
مميزات منتج سيجما بلوت
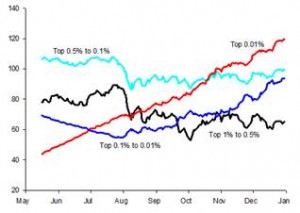
مؤامرة الغابات
مخطط الغابة هو أحد أشكال "التحليل التلوي" الذي يستخدم للجمع بين تحليلات متعددة تتناول نفس السؤال. يجمع التحليل التلوي إحصائيًا عينات كل دراسة مساهمة لإنشاء إحصائية موجزة شاملة أكثر دقة من حجم التأثير في الدراسات الفردية. تظهر قيم الدراسة الفردية وفترات الثقة 95% الخاصة بها كرموز مربعة مع أشرطة خطأ أفقية وإحصائيات الملخص الإجمالي على شكل معين بعرض يساوي فاصل الثقة 95% الخاص بها.

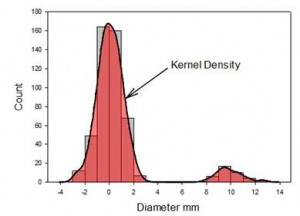
كثافة النواة
ستقوم ميزة كثافة النواة بإنشاء تقدير لتوزيع البيانات الأساسية. وينبغي مقارنة ذلك بالرسم البياني الشبيه بالخطوة. وله مزايا (بدون أشرطة) وعيوب (فقدان معلومات العدد) مقارنة بالرسم البياني ويجب استخدامه مع الرسم البياني. يمكن إنشاؤها في وقت واحد.
كثافة النقطة مع أشرطة الخطأ المتوسطة والمعيارية
تمت إضافة المتوسط بالإضافة إلى حساب شريط الخطأ القياسي، والرمز بالإضافة إلى أشرطة الخطأ، إلى الرسم البياني لكثافة النقاط. يؤدي هذا إلى تحسين إحصائيات عرض كثافة النقاط المحتملة الأخرى - المتوسط والوسيط والنسب المئوية وboxplot.

مخططات الألوان
تم تنفيذ عشرة أنظمة ألوان جديدة. ثلاثة أمثلة موضحة أدناه:
تحسينات الأسطورة – الأشكال
تتوفر الآن أشكال الأسطورة الرأسية والأفقية والمستطيلة.
عكس ترتيب الأسطورة
يمكنك الآن تحديد عكس ترتيب عناصر وسيلة الإيضاح. يوفر هذا ترتيبًا أكثر منطقية لبعض أنواع الرسوم البيانية.
إعادة ترتيب العناصر الأسطورية
هناك ثلاث طرق لإعادة ترتيب عناصر وسيلة الإيضاح. كما هو موضح هنا، يمكنك نقل عنصر واحد أو عدة عناصر إيضاحية لأعلى أو لأسفل باستخدام عناصر تحكم السهم لأعلى/لأسفل في لوحة وسائل الإيضاح في خصائص الرسم البياني. والأسهل من ذلك، ما عليك سوى تحديد العنصر الموجود في وسيلة الإيضاح واستخدام مفاتيح الأسهم لأعلى ولأسفل على لوحة المفاتيح. أو حدد عنصر وسيلة الإيضاح واسحبه إلى الموضع الجديد باستخدام مؤشر الماوس.
تحرير شريط الأدوات المصغر لعناصر وسيلة الإيضاح
يمكن الآن تحرير عناصر وسيلة الإيضاح بالنقر فوق العنصر واستخدام شريط الأدوات المصغر.

وضع العلامات المباشرة
يمكن الآن فك تجميع وسيلة الإيضاح ووضع عناصر وسيلة الإيضاح الفردية بجوار المخططات المناسبة. ستتحرك التسميات مع الرسم البياني للحفاظ على موضعها بالنسبة للرسم البياني. نظرًا لأن الملصق مجاور لقطعة الأرض، فقد أصبح التعرف البصري على كل قطعة أرض أسهل بكثير الآن.
تحليل المكونات الرئيسية (PCA)

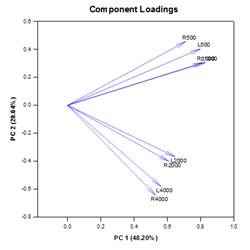
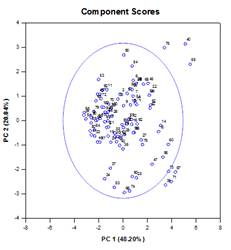
تحليل المكون الرئيسي (PCA) هو أسلوب لتقليل تعقيد البيانات عالية الأبعاد عن طريق تقريب البيانات بأبعاد أقل. ويسمى كل بعد جديد مكونًا رئيسيًا ويمثل مزيجًا خطيًا من المتغيرات الأصلية. يمثل المكون الرئيسي الأول أكبر قدر ممكن من الاختلاف في البيانات. يمثل كل مكون رئيسي لاحق أكبر قدر ممكن من التباين المتبقي ويكون متعامدًا مع جميع المكونات الرئيسية السابقة.
يمكنك فحص المكونات الرئيسية لفهم مصادر الاختلاف في بياناتك. يمكنك أيضًا استخدامها في تكوين نماذج تنبؤية. إذا كان معظم الاختلاف في بياناتك موجودًا في مجموعة فرعية منخفضة الأبعاد، فقد تتمكن من تصميم متغير الاستجابة الخاص بك من حيث المكونات الرئيسية. يمكنك استخدام المكونات الأساسية لتقليل عدد المتغيرات في الانحدار والتجميع والتقنيات الإحصائية الأخرى.
يمكنك فحص المكونات الرئيسية لفهم مصادر الاختلاف في بياناتك. يمكنك أيضًا استخدامها في تكوين نماذج تنبؤية. إذا كان معظم الاختلاف في بياناتك موجودًا في مجموعة فرعية منخفضة الأبعاد، فقد تتمكن من تصميم متغير الاستجابة الخاص بك من حيث المكونات الرئيسية. يمكنك استخدام المكونات الأساسية لتقليل عدد المتغيرات في الانحدار والتجميع والتقنيات الإحصائية الأخرى.
يتكون الإخراج الرسومي من مخططات Scree وتحميل المكونات ونتائج المكونات.
تحليل التباين (ANCOVA)
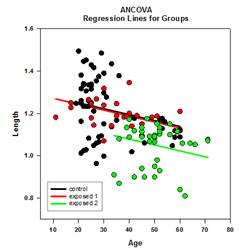
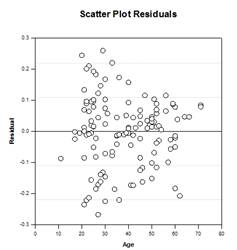
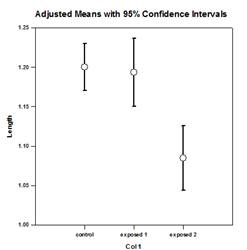
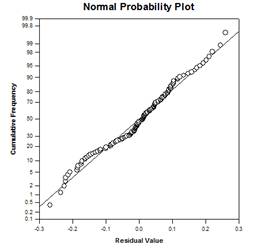
يعتمد نموذج تحليل التباين (ANOVA) أحادي العامل على تصميم عشوائي تمامًا يتم فيه أخذ عينات عشوائية من أفراد الدراسة من مجتمع ما ثم يتم تعيين كل موضوع بشكل عشوائي إلى واحد من مستويات العوامل أو المعالجات المتعددة بحيث يكون لكل موضوع احتمال متساوٍ لـ تلقي العلاج. الافتراض الشائع لهذا التصميم هو أن الموضوعات متجانسة. وهذا يعني أن أي متغير آخر، حيث توجد اختلافات بين الأشخاص، لا يغير تأثير العلاج بشكل كبير ولا يلزم إدراجه في النموذج. ومع ذلك، غالبًا ما تكون هناك متغيرات، خارجة عن سيطرة الباحث، تؤثر على الملاحظات داخل مجموعة عامل واحدة أو أكثر، مما يؤدي إلى التعديلات اللازمة في متوسطات المجموعة، وأخطائها، ومصادر التباين، والقيم P لتأثير المجموعة، بما في ذلك مقارنات متعددة.
وتسمى هذه المتغيرات المتغيرات المشتركة. وهي عادةً متغيرات مستمرة، ولكن يمكن أيضًا أن تكون قاطعة. وبما أنها عادة ما تكون ذات أهمية ثانوية للدراسة، وكما ذكرنا أعلاه، لا يمكن السيطرة عليها من قبل الباحث، فإنها لا تمثل عوامل تأثيرات رئيسية إضافية، ولكن لا يزال من الممكن تضمينها في النموذج لتحسين دقة النتائج. تُعرف المتغيرات المشتركة أيضًا باسم المتغيرات المزعجة أو المتغيرات المصاحبة.
تحليل التباين المشترك (ANCOVA) هو امتداد لتحليل التباين (ANOVA) الذي يتم الحصول عليه عن طريق تحديد واحد أو أكثر من المتغيرات المشتركة كمتغيرات إضافية في النموذج. إذا قمت بترتيب بيانات تحليل التباين (ANCOVA) في ورقة عمل SigmaPlot باستخدام تنسيق البيانات المفهرسة، فسيمثل عمود واحد العامل وسيمثل عمود واحد المتغير التابع (الملاحظات) كما في تصميم تحليل التباين (ANOVA). بالإضافة إلى ذلك، سيكون لديك عمود واحد لكل متغير مشترك. عند استخدام نموذج يتضمن تأثيرات المتغيرات المشتركة، يكون هناك تباين أكثر وضوحًا في قيمة المتغير التابع.
يؤدي هذا بشكل عام إلى تقليل التباين غير المفسر الذي يعزى إلى تباين العينات العشوائية، مما يزيد من حساسية تحليل التباين المشترك (ANCOVA) مقارنة بنفس النموذج بدون متغيرات مشتركة (نموذج تحليل التباين المشترك). تعني حساسية الاختبار الأعلى أن فروق المتوسط الأصغر بين المعالجات ستصبح ذات دلالة إحصائية مقارنة بنموذج ANOVA القياسي، وبالتالي زيادة القوة الإحصائية.
كمثال بسيط لاستخدام تحليل التباين المشترك (ANCOVA)، فكر في تجربة يتم فيها تعيين الطلاب بشكل عشوائي إلى واحد من ثلاثة أنواع من أساليب التدريس ويتم قياس درجات إنجازاتهم. الهدف هو قياس تأثير الطرق المختلفة وتحديد ما إذا كانت إحدى الطرق تحقق متوسط درجات أعلى بكثير من الطرق الأخرى. الأساليب هي المحاضرة، والتعلم الذاتي، والتعلم التعاوني. يؤدي إجراء تحليل التباين الأحادي (One Way ANOVA) على هذه البيانات الافتراضية إلى الحصول على النتائج في الجدول أدناه، تحت عنوان عمود تحليل التباين (ANOVA). ونستنتج أنه لا يوجد فرق كبير بين طرق التدريس. لاحظ أيضًا أن التباين غير المفسر بواسطة نموذج ANOVA والذي يرجع إلى تباين العينات العشوائية في الملاحظات يقدر بـ 35.17.
ومن الممكن أن يستفيد الطلاب في دراستنا من إحدى الطرق أكثر من الطرق الأخرى، بناءً على أدائهم الأكاديمي السابق. لنفترض أننا قمنا بتحسين الدراسة لتشمل متغيرًا مشتركًا يقيس بعض القدرات السابقة، مثل التقييم القائم على المعايير (SBA) المعتمد من الدولة. يؤدي إجراء تحليل التباين الأحادي (ANCOVA) على هذه البيانات إلى الحصول على النتائج في الجدول أدناه، تحت عنوان عمود تحليل التباين (ANCOVA).
المتوسط المعدل الوارد في الجدول لكل طريقة هو تصحيح لمتوسط المجموعة للتحكم في تأثيرات المتغير المشترك. أظهرت النتائج أن الوسائل المعدلة تختلف بشكل كبير مع طريقة المحاضرة باعتبارها الأكثر نجاحا. لاحظ كيف انخفضت الأخطاء المعيارية للمتوسطات بمقدار ثلاثة أضعاف تقريبًا بينما انخفض التباين الناتج عن تقلب العينة العشوائية بمقدار عشرة أضعاف. إن تقليل الخطأ هو النتيجة المعتادة لإدخال المتغيرات المشتركة وإجراء تحليل تحليل التباين (ANCOVA).
هناك أربعة رسوم بيانية لنتائج تحليل التباين (ANCOVA) - خطوط الانحدار في المجموعات، والمخطط المبعثر للبقايا، والوسائل المعدلة بفواصل الثقة، ومخطط الاحتمالية الطبيعية:
قيم P لـ ANOVAs غير البارامترية
اختبارات ANOVA غير البارامترية في SigmaPlot هي اختبار Kruskal-Wallis (تحليل التباين أحادي الاتجاه في الرتب) واختبار فريدمان (تحليل التباين أحادي الاتجاه للقياسات المتكررة في الرتب). يوفر كلاهما أربعة إجراءات اختبار ما بعد المخصص لتحديد مصدر التأثيرات الهامة في عامل العلاج. الإجراءات الأربعة هي Tukey وSNK وDunn's وDunnett's.
يمكن استخدام الإجراءات الثلاثة الأولى لاختبار أهمية كل مقارنة زوجية لمجموعات العلاج، في حين يمكن استخدام الإجراءين الأخيرين لاختبار أهمية المقارنات مع مجموعة المراقبة. طريقة دان هي الإجراء الوحيد المتاح إذا كانت مجموعات العلاج لديها أحجام عينات غير متساوية.
عند استخدام إجراء الاختبار اللاحق، يتم تقديم جدول في التقرير يسرد نتائج المقارنات الزوجية لمستويات العلاج. يوضح العمود الأخير من الجدول ما إذا كان الفرق في الرتب كبيرًا أم لا. في الإصدارات السابقة من SigmaPlot، لم تكن هناك قيمة p معدلة يمكن مقارنتها بمستوى أهمية ANOVA (عادة 0.05) لتحديد الأهمية.
وذلك لأن SigmaPlot كان يحدد الأهمية من خلال مقارنة إحصائية الاختبار المرصودة، المحسوبة لكل مقارنة، بالقيمة الحرجة لتوزيع الإحصائية التي يتم الحصول عليها من جدول البحث. كان لدى SigmaPlot مجموعتان من جداول البحث للتوزيعات الاحتمالية المقابلة للطرق الأربعة اللاحقة، حيث كانت مجموعة واحدة لمستوى أهمية قدره 0.05 ومجموعة أخرى لمستوى أهمية قدره 0.01.
تم تغيير هذا مؤخرًا لاستخدام الإجراءات التحليلية لحساب القيم الاحتمالية لهذه التوزيعات، مما يجعل جداول البحث قديمة. وبسبب هذا التغيير، أصبحنا الآن قادرين على الإبلاغ عن القيم الاحتمالية المعدلة لكل مقارنة زوجية. يتيح هذا التغيير أيضًا إزالة القيود المفروضة على استخدام .05 و.01 كمستويات الأهمية الوحيدة للمقارنات المتعددة. وبالتالي يمكن للمستخدم إدخال أي مستوى أهمية صالح لقيمة P من 0 إلى 1.
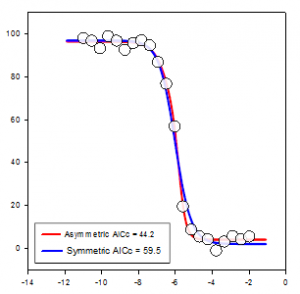
معيار المعلومات Akaike (AICc)
يوفر معيار معلومات Akaike (AIC) طريقة لقياس الأداء النسبي في ملاءمة نموذج الانحدار لمجموعة معينة من البيانات. يعتمد هذا المعيار على مفهوم إنتروبيا المعلومات، ويقدم قياسًا نسبيًا للمعلومات المفقودة عند استخدام نموذج لوصف البيانات. وبشكل أكثر تحديدًا، فإنه يعطي مقايضة بين تعظيم احتمالية النموذج المقدر (مثل تقليل مجموع المربعات المتبقية إذا كانت البيانات موزعة بشكل طبيعي) والحفاظ على عدد المعلمات الحرة في النموذج إلى الحد الأدنى، مما يقلل من تعقيده. على الرغم من أن جودة الملاءمة يتم تحسينها دائمًا تقريبًا عن طريق إضافة المزيد من المعلمات، إلا أن التجاوز سيزيد من حساسية النموذج للتغيرات في البيانات المدخلة ويمكن أن يدمر قدرته التنبؤية.
السبب الأساسي لاستخدام AIC هو كدليل لاختيار النموذج. ومن الناحية العملية، يتم حسابها لمجموعة من النماذج المرشحة ومجموعة بيانات معينة. يتم تحديد النموذج ذو أصغر قيمة لـ AIC باعتباره النموذج في المجموعة الذي يمثل النموذج "الحقيقي" على أفضل وجه، أو النموذج الذي يقلل من فقدان المعلومات، وهو ما تم تصميم AIC لتقديره. بعد تحديد النموذج الذي يحتوي على الحد الأدنى من AIC، يمكن أيضًا حساب الاحتمالية النسبية لكل نموذج من النماذج المرشحة الأخرى لقياس احتمال تقليل فقدان المعلومات مقارنة بالنموذج الذي يحتوي على الحد الأدنى من AIC. يمكن أن يساعد الاحتمال النسبي المحقق في تحديد ما إذا كان ينبغي الاحتفاظ بأكثر من نموذج واحد في المجموعة لمزيد من الدراسة.
يعتمد حساب AIC على الصيغة العامة التالية التي حصلت عليها Akaike
يتبين أن AICc يفرض عقوبة أكبر من AIC عندما تكون هناك معلمات إضافية. يبدو أن معظم المؤلفين متفقون على ضرورة استخدام AICc بدلاً من AIC في جميع المواقف، ويتم تنفيذ AICc في SigmaPlot. تعد المعادلة غير المتماثلة في الرسم البياني أفضل بكثير من المعادلة المتماثلة نظرًا لأن قيمة AICc الخاصة بها أقل بمقدار 7 وحدات من المعادلة المتماثلة - وهي قاعدة أساسية لـ AICc. إذا كان الفرق أكبر من 2، فإن المعادلة ذات قيمة AICc الأصغر لا ينبغي اعتبارها الأفضل بل مرشحة لأفضل معادلة.
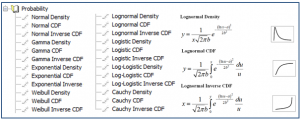
وظائف احتمالية الانحدار غير الخطية
تمت إضافة 24 دالة احتمالية جديدة إلى مكتبة الملاءمة القياسية.jfl. هذه الوظائف وبعض المعادلات والأشكال الرسومية مبينة أدناه.
وظائف الترجيح الانحدار غير الخطية
توجد الآن سبع وظائف ترجيح مختلفة مدمجة في كل معادلة انحدار غير خطية (تختلف الأبعاد الثلاثية قليلاً). هذه الوظائف هي متبادل y، متبادل y تربيع، مقلوب x، مقلوب x تربيع، توقعات متبادلة، توقعات متبادلة تربيعية و كوشي. يتم استخدام خوارزمية المربعات الصغرى المعاد وزنها بشكل متكرر للسماح بتغيير الأوزان أثناء كل تكرار انحدار غير خطي. وبهذه الطريقة، يمكن الحصول على "الترجيح بالتنبؤات"، وهي طريقة شائعة الاستخدام، عن طريق تحديد خيار الترجيح reciprocal_pred.

أيضًا، يمكن استخدام ترجيح كوشي (اختر الوزن_كوشي) لملاءمة معادلة للبيانات التي تحتوي على القيم المتطرفة وسيتم تقليل تأثير القيم المتطرفة. يمكن للمستخدمين إنشاء طرق الوزن الخاصة بهم من حيث المخلفات و/أو المعلمات لتنفيذ طرق تركيب قوية أخرى. يتم عرض قسم المعادلة في ملف مناسب مع وظائف الترجيح السبعة المضمنة.
ميزات واجهة المستخدم - إعادة ترتيب العناصر في دفتر الملاحظات الخاص بك عن طريق السحب
لا يتم بالضرورة إنشاء الكائنات الموجودة في قسم دفتر الملاحظات بترتيب منطقي. يمكنك الآن سحب العناصر الموجودة داخل القسم إلى مواضع جديدة لوضعها بشكل أكثر منطقية.
برنامج تعليمي محدث لـ SigmaPlot
البرنامج التعليمي الجديد يجعل إنشاء الرسوم البيانية لأول مرة أمرًا سهلاً. يبدأ بأمثلة بسيطة ويصبح تدريجيًا أكثر تعقيدًا.

تحديد عرض خط الرسم من عمود ورقة العمل
يمكن الآن إدخال قيم عرض الخط في عمود ورقة العمل. يمكن استخدام هذه القيم ضمن رسم بياني أو عبر رسوم بيانية متعددة على الصفحة.
تنسيقات ملفات التصدير المتجهية
تمت إضافة تنسيقات ملفات SVG (رسومات متجهة قابلة للتحجيم) وSWF (Adobe Flash Player) وتنسيقات ملفات Vector PDF. هذه تنسيقات قابلة للتطوير حيث لا يتم فقدان أي دقة عند التكبير/التصغير إلى مستويات مختلفة. SVG هو تنسيق الرسومات القياسي للويب ويمكن استخدام SWF مع Adobe Flash Player. نظرًا لاستخدام pdf بشكل متكرر، أصبح تنسيق PDF المتجه الآن مرفقًا بالزر "إنشاء PDF" الموجود على الشريط الرئيسي.
تحديث تنسيقات ملفات التطبيق
تم تحديث دعم استيراد وتصدير الملفات إلى الإصدارين 13 و14 من Minitab، والإصدار 9 من SAS والإصدار 19 من SPSS.