Allgemeine Merkmale
Neue Funktionen
Im Jahr 2007 wurden die Funktionen und Merkmale von SigmaStat ab Version 11 in SigmaPlot integriert. Am 1. Februar 2016 wurde jedoch SigmaStat 4.0 veröffentlicht und ist nun als eigenständiges Produkt erhältlich.
Nachfolgend finden Sie die zahlreichen Verbesserungen der statistischen Analysefunktionen in SigmaStat:
- Hauptkomponentenanalyse (PCA) - Die Hauptkomponentenanalyse ist eine Technik zur Verringerung der Komplexität hochdimensionaler Daten durch Annäherung der Daten mit weniger Dimensionen.
- Kovarianzanalyse (ANCOVA) - Die Kovarianzanalyse ist eine Erweiterung der ANOVA (Varianzanalyse), bei der eine oder mehrere Kovariaten als zusätzliche Variablen in das Modell aufgenommen werden.
- Cox-Regression - Dies umfasst das proportionale Risikomodell mit Stratifizierung zur Untersuchung der Auswirkungen potenzieller Risikofaktoren auf die Überlebenszeit einer Population. Die Eingabedaten können kategorisch sein.
- T-Test für eine Stichprobe - Testet die Hypothese, dass der Mittelwert einer Grundgesamtheit gleich einem bestimmten Wert ist.
- Odds-Ratio- und Relativ-Risiko-Tests - Beide testen die Hypothese, dass eine Behandlung keinen Einfluss auf die Häufigkeit des Auftretens eines bestimmten Ereignisses in einer Population hat. Die Odds Ratio wird in retrospektiven Studien verwendet, um den Behandlungseffekt zu bestimmen, nachdem das Ereignis beobachtet wurde. Das relative Risiko wird in prospektiven Studien verwendet, bei denen die Behandlungs- und die Kontrollgruppe bereits vor Eintritt des Ereignisses ausgewählt wurden.
- Shapiro-Wilk-Normalitätstest - Ein genauerer Test als Kolmogorov-Smirnov zur Beurteilung der Normalität von Stichprobendaten. Wird bei der Überprüfung von Annahmen für viele statistische Tests verwendet, kann aber auch direkt auf Arbeitsblattdaten angewendet werden.
- Neue Ergebnisgrafik - ANOVA-Profildiagramme: Dient zur Analyse der Haupteffekte und Wechselwirkungen höherer Ordnung von Faktoren in einem ANOVA-Multifaktorentwurf durch Vergleich der Mittelwerte der kleinsten Quadrate.
- Neue Wahrscheinlichkeitstransformationen - Vierunddreißig neue Funktionen wurden der Transform-Sprache von SigmaStat hinzugefügt, um Wahrscheinlichkeiten und Werte zu berechnen, die mit Verteilungen verbunden sind, die in vielen Studienbereichen auftreten.
- Neue Schnittstellenänderung - Nichtlineare Regression: Eine einfach zu bedienende Assistentenoberfläche und detailliertere Berichte.
- Neue Schnittstellenänderung - Schnelltransformationen: Eine einfachere Methode zur Durchführung von Berechnungen im Arbeitsblatt.
- Änderung der Benutzeroberfläche - Neue Benutzeroberfläche: Ermöglicht dem Benutzer, einfacher mit Excel-Arbeitsblättern zu arbeiten.
- Yates-Korrektur zusätzlich zum Mann-Whitney-Test - Die Yates-Korrektur für Kontinuität oder der Yates-Chi-Quadrat-Test wird verwendet, wenn in einer Kontingenztabelle auf Unabhängigkeit getestet wird, um zu beurteilen, ob zwei Stichproben von Beobachtungen aus der gleichen Verteilung stammen.
- Verbesserte Fehlermeldungen - Verbesserte Fehlermeldungen haben Informationen hinzugefügt, wenn die Überprüfung von Annahmen für ANOVA fehlgeschlagen ist.
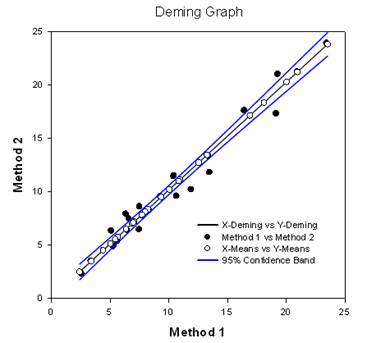
- Deming-Regression - Die Deming-Regression berücksichtigt Fehler sowohl bei den X- als auch bei den Y-Variablen - eine Technik für den Methodenvergleich, bei der die X-Daten von einer Methode und die Y-Daten von der anderen stammen. Die Deming-Regressionsmethode erweitert im Grunde die normale lineare Regression, bei der die X-Werte als fehlerfrei angesehen werden, auf den Fall, dass sowohl X als auch Y (beide Methoden) Fehler aufweisen. Anschließend können die Hypothesen getestet werden, z. B. die Steigung von 1,0, um festzustellen, ob die Methoden gleich sind. So könnten beispielsweise zwei Geräte zur Messung derselben Substanz oder zwei algorithmische Methoden zur Erkennung von Tumoren in Bildern miteinander verglichen werden. Das Diagramm vergleicht die beiden Methoden, um festzustellen, ob sie unterschiedlich oder gleich sind. Ein Bericht enthält statistische Ergebnisse.
- Akaike Information Criterion (AICc) - Das Akaike Information Criterion ist jetzt in Berichten über nichtlineare Regression verfügbar. Es handelt sich um ein Kriterium für die Anpassungsgüte, das auch die Anzahl der Parameter in der Gleichung berücksichtigt. Sie gilt auch für nicht verschachtelte Gleichungen, wie sie z. B. bei der Analyse der Enzymkinetik auftreten.
- Neue Wahrscheinlichkeitsfunktionen für nichtlineare Regression - Insgesamt 24 Wahrscheinlichkeitsfunktionen wurden der Kurvenanpassungsbibliothek hinzugefügt. Für jede wurde eine automatische Gleichung für die erste Parameterschätzung erstellt.
- Nichtlineare Regressionsgewichtung - Es gibt jetzt sieben verschiedene Gewichtungsfunktionen, die in jede nichtlineare Regressionsgleichung eingebaut sind (3D ist leicht unterschiedlich). Diese Funktionen sind reziprok y, reziprok y zum Quadrat, reziprok x, reziprok x zum Quadrat, reziprok predicteds, reziprok predicteds zum Quadrat und Cauchy. Der Algorithmus der iterativ neu gewichteten kleinsten Quadrate wird verwendet, damit sich die Gewichte während jeder Iteration der nichtlinearen Regression ändern können.
- Verbesserungen beim Mehrfachvergleichstest - Es wurden zwei wichtige Verbesserungen vorgenommen. Die P-Werte für die Ergebnisse der nichtparametrischen ANOVA wurden hinzugefügt. Diese gab es vorher nicht. Auch die P-Werte für Mehrfachvergleiche waren auf diskrete Auswahlmöglichkeiten beschränkt (0,05, 0,01 usw.). Diese Einschränkung besteht nicht mehr und es kann jeder gültige P-Wert verwendet werden.
Wichtige neue statistische Tests
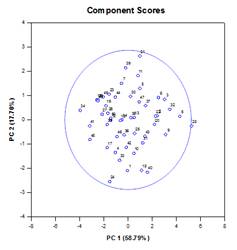
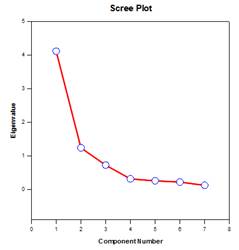
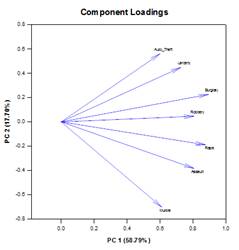
Hauptkomponentenanalyse (PCA) – DieHauptkomponentenanalyse ist eine Technik zur Verringerung der Komplexität hochdimensionaler Daten durch Annäherung der Daten mit weniger Dimensionen. Jede neue Dimension wird als Hauptkomponente bezeichnet und stellt eine lineare Kombination der ursprünglichen Variablen dar. Die erste Hauptkomponente berücksichtigt so viel Variation in den Daten wie möglich. Jede nachfolgende Hauptkomponente berücksichtigt so viel der verbleibenden Variation wie möglich und ist orthogonal zu allen vorherigen Hauptkomponenten.
Sie können Hauptkomponenten untersuchen, um die Quellen der Variation in Ihren Daten zu verstehen. Sie können sie auch zur Erstellung von Vorhersagemodellen verwenden. Wenn der größte Teil der Variation in Ihren Daten in einer niedrigdimensionalen Teilmenge vorliegt, können Sie Ihre Antwortvariable möglicherweise anhand der Hauptkomponenten modellieren. Sie können Hauptkomponenten verwenden, um die Anzahl der Variablen bei Regression, Clustering und anderen statistischen Verfahren zu reduzieren. Das Hauptziel der Hauptkomponentenanalyse besteht darin, die Quellen der Variabilität in den Daten zu erklären und die Daten mit weniger Variablen darzustellen, wobei der größte Teil der Gesamtvarianz erhalten bleibt.
Beispiele für Hauptkomponenten-Diagramme:
Kovarianzanalyse (ANCOVA) – DieKovarianzanalyse ist eine Erweiterung der ANOVA, bei der eine oder mehrere Kovariaten als zusätzliche Variablen in das Modell aufgenommen werden. Wenn Sie ANCOVA-Daten in einem SigmaPlot-Arbeitsblatt unter Verwendung des indizierten Datenformats anordnen, steht eine Spalte für den Faktor und eine Spalte für die abhängige Variable (die Beobachtungen), wie in einem ANOVA-Design. Außerdem haben Sie eine Spalte für jede Kovariate.
Beispiele für ANCOVA-Diagramme:
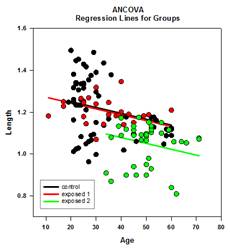
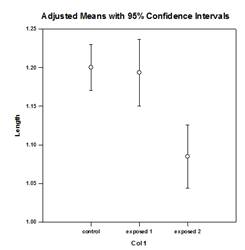
Neue statistische Merkmale
Verbesserungen bei Mehrfachvergleichen – Die P-Wert-Berechnung bei Mehrfachvergleichen wurde erheblich verbessert. Die folgenden Mehrfachvergleichsverfahren, Tukey (nicht-parametrische Tests), SNK (nicht-parametrische Tests), Dunnett’s, Dunn’s (nur nicht-parametrische Tests) und Duncan berechneten die p-Werte nicht analytisch, sondern benutzten Nachschlagetabellen mit kritischen Werten für eine bestimmte Verteilung, um, gegebenenfalls durch Interpolation, festzustellen, ob eine berechnete Teststatistik einen signifikanten Unterschied in den Gruppenmitteln darstellt. Daher wurden für diese Tests keine p-Werte angegeben, sondern nur die Schlussfolgerung, ob ein signifikanter Unterschied besteht oder nicht. Ein großes Problem bei diesem Ansatz ist, dass die Nachschlagetabellen nur für zwei Signifikanzniveaus, nämlich .05 und .01, verfügbar sind. Ein weiteres Problem ist, dass viele Kunden die p-Werte wissen wollen. Für SigmaPlot wurden Algorithmen kodiert, um die Verteilungen für die Teststatistiken für alle Post-Hoc-Prozeduren zu berechnen, wodurch die Nachschlagetabellen obsolet werden. Infolgedessen werden nun bereinigte p-Werte für alle Post-hoc-Verfahren in den Bericht aufgenommen. Außerdem ist es nicht mehr erforderlich, das Signifikanzniveau bei Mehrfachvergleichen auf 0,05 oder 0,01 zu beschränken. Stattdessen ist das Signifikanzniveau der Mehrfachvergleiche dasselbe wie das Signifikanzniveau des Haupttests (Omnibus). Für diesen p-Wert gibt es keine Beschränkung – es kann jeder gültige Wert verwendet werden.
Akaike-Informationskriterium (AICc ) – Das Akaike-Informationskriterium wurde den Berichten des Regressionsassistenten und des Assistenten für dynamische Anpassung sowie dem Dialogfeld Berichtsoptionen hinzugefügt. Sie bietet eine Methode zur Messung der relativen Leistung bei der Anpassung eines Regressionsmodells an einen bestimmten Datensatz. Das Kriterium basiert auf dem Konzept der Informationsentropie und bietet ein relatives Maß für den Informationsverlust bei der Verwendung eines Modells zur Beschreibung der Daten.
Genauer gesagt ist es ein Kompromiss zwischen der Maximierung der Wahrscheinlichkeit für das geschätzte Modell (das entspricht der Minimierung der Summe der Residuenquadrate, wenn die Daten normalverteilt sind) und der Minimierung der Anzahl der freien Parameter im Modell, wodurch dessen Komplexität reduziert wird. Obwohl die Anpassungsgüte fast immer durch das Hinzufügen weiterer Parameter verbessert wird, erhöht sich durch eine Überanpassung die Empfindlichkeit des Modells gegenüber Änderungen der Eingabedaten und kann seine Vorhersagefähigkeit beeinträchtigen.
Der Hauptgrund für die Verwendung von AIC ist die Orientierung bei der Modellauswahl. In der Praxis wird sie für eine Reihe von Modellkandidaten und einen bestimmten Datensatz berechnet. Das Modell mit dem kleinsten AIC-Wert wird als das Modell in der Menge ausgewählt, das das “wahre” Modell am besten repräsentiert, oder das Modell, das den Informationsverlust minimiert, was das Ziel der AIC-Schätzung ist.
Nachdem das Modell mit dem minimalen AIC ermittelt wurde, kann auch eine relative Wahrscheinlichkeit für jedes der anderen in Frage kommenden Modelle berechnet werden, um die Wahrscheinlichkeit der Verringerung des Informationsverlusts im Vergleich zum Modell mit dem minimalen AIC zu messen. Die relative Wahrscheinlichkeit kann dem Untersucher bei der Entscheidung helfen, ob mehr als ein Modell in der Menge für die weitere Betrachtung beibehalten werden sollte.
Die Berechnung des AIC basiert auf der folgenden, von Akaike1 aufgestellten allgemeinen Formel
![]()
wobei ![]() die Anzahl der freien Parameter im Modell und
die Anzahl der freien Parameter im Modell und ![]() der maximierte Wert der Likelihood-Funktion für das geschätzte Modell ist.
der maximierte Wert der Likelihood-Funktion für das geschätzte Modell ist.
Wenn der Stichprobenumfang der Daten ![]() im Verhältnis zur Anzahl der Parameter
im Verhältnis zur Anzahl der Parameter![]() klein ist (einige Autoren sagen, wenn
klein ist (einige Autoren sagen, wenn ![]() nicht mehr als ein paar Mal größer als
nicht mehr als ein paar Mal größer als ![]() ist), kann AIC nicht so gut vor Overfitting schützen. In diesem Fall gibt es eine korrigierte Version des AIC, die durch gegeben ist:
ist), kann AIC nicht so gut vor Overfitting schützen. In diesem Fall gibt es eine korrigierte Version des AIC, die durch gegeben ist:
![]()
Es zeigt sich, dass AICc einen größeren Nachteil als AIC auferlegt, wenn es zusätzliche Parameter gibt. Die meisten Autoren scheinen sich einig zu sein, dass AICc in allen Situationen anstelle von AIC verwendet werden sollte.
Wahrscheinlichkeits-Fit-Funktionen – 24 neue Wahrscheinlichkeits-Fit-Funktionen wurden der Fit-Bibliothek standard.jfl hinzugefügt. Diese Funktionen sowie einige Gleichungen und Diagrammformen sind unten dargestellt:

Als Beispiel enthält die Fit-Datei für die Lognormal-Dichte-Funktion die Gleichung für die Lognormal-Dichte lognormden(x,a,b), Gleichungen für die automatische Anfangsparameterschätzung und die sieben neuen Gewichtungsfunktionen.
[Variables]
x = Spalte(1)
y = col(2)
reziprok_y = 1/abs(y)
Kehrwert_Quadrat = 1/y^2
reziprok_x = 1/abs(x)
reziprok_xQuadrat = 1/x^2
reziprok_pred = 1/abs(f)
reziproker_Predsqr = 1/f^2
Gewicht_Cauchy = 1/(1+4*(y-f)^2)
Automatische Funktionen zur Schätzung der Anfangsparameter
trap(q,r)=.5*Gesamt(({0,q}+{q,0})[data(2,size(q))]*diff(r)[data(2,size(r))])
s=sort(komplex(x,y),x)
u = Unterblock(s,1,1,1, Größe(x))
v = subblock(s,2,1,2, size(y))
Mittelwert = Trap(u*v,u)
varest=trap((u-mittelwert)^2*v,u)
p = 1+varest/meanest^2
[Parameters]
a= if(Mittelwert > 0, ln(Mittelwert/sqrt(p)), 0)
b= if(p >= 1, sqrt(ln(p)), 1)
[Equation]
f=lognormden(x,a,b)
f an y anpassen
“f an y mit dem Gewicht reciprocal_y anpassen
“f an y anpassen mit Gewicht reziprok_Quadrat
“f an y anpassen mit Gewicht reziprok_x
“f an y mit dem Gewicht reciprocal_xsquare anpassen
“f an y anpassen mit Gewicht reziprok_pred
“f an y anpassen mit Gewicht reciprocal_predsqr
“f an y anpassen mit Gewicht Gewicht_Cauchy
[Constraints]
b>0
[Options]
Toleranz=1e-010
Schrittweite=1
Iterationen=200
Gewichtungsfunktionen in der nichtlinearen Regression – SigmaPlot Gleichungselemente verwenden manchmal eine Gewichtsvariable, um jeder Beobachtung (oder Antwort) in einem Regressionsdatensatz ein Gewicht zuzuweisen. Das Gewicht einer Beobachtung misst ihre Unsicherheit in Bezug auf die Wahrscheinlichkeitsverteilung, aus der sie entnommen wurde. Ein größeres Gewicht weist auf eine Beobachtung hin, die nur wenig vom wahren Mittelwert ihrer Verteilung abweicht, während ein kleineres Gewicht auf eine Beobachtung hinweist, die stärker aus dem Schwanzbereich ihrer Verteilung abgetastet wurde.
Unter den statistischen Annahmen für die Schätzung der Parameter eines angepassten Modells mit Hilfe der Methode der kleinsten Quadrate sind die Gewichte bis zu einem Skalierungsfaktor gleich dem Kehrwert der Varianzen der Populationen der (Gaußschen) Verteilungen, aus denen die Beobachtungen entnommen werden. Hier definieren wir ein Residuum, das manchmal auch als Rohresiduum bezeichnet wird, als die Differenz zwischen einer Beobachtung und dem vorhergesagten Wert (dem Wert des angepassten Modells) bei einem bestimmten Wert der unabhängigen Variable(n). Wenn die Varianzen der Beobachtungen nicht alle gleich sind(Heteroskedastizität), wird eine Gewichtungsvariable benötigt, und das Problem der gewichteten kleinsten Quadrate, das darin besteht, die gewichtete Summe der Quadrate der Residuen zu minimieren, wird gelöst, um die besten Anpassungsparameter zu finden.
Unsere neue Funktion ermöglicht es dem Benutzer, eine Gewichtungsvariable als Funktion der im Anpassungsmodell enthaltenen Parameter zu definieren. Sieben vordefinierte Gewichtungsfunktionen wurden zu jeder Anpassungsfunktion hinzugefügt (3D-Funktionen sind leicht unterschiedlich). Die sieben unten aufgeführten sind 1/y, 1/y2, 1/x, 1/x2, 1/vorgesagt, 1/vorgesagt2 und Cauchy.

Eine Anwendung dieser allgemeineren adaptiven Gewichtung ist in Situationen, in denen die Varianzen der Beobachtungen vor der Durchführung der Anpassung nicht bestimmt werden können. Wenn zum Beispiel alle Beobachtungen Poisson-verteilt sind, dann sind die Mittelwerte der Population, die durch die vorhergesagten Werte geschätzt werden, gleich den Varianzen der Population. Obwohl die Methode der kleinsten Quadrate zur Schätzung von Parametern für normalverteilte Daten konzipiert ist, werden manchmal auch andere Verteilungen mit kleinsten Quadraten verwendet, wenn andere Methoden nicht verfügbar sind. Im Falle von Poisson-Daten muss die Gewichtsvariable als Kehrwert der vorhergesagten Werte definiert werden. Dieses Verfahren wird manchmal auch als “Gewichtung nach vorhergesagten Werten” bezeichnet.
Eine weitere Anwendung der adaptiven Gewichtung besteht darin, robuste Verfahren zur Schätzung von Parametern zu erhalten, die die Auswirkungen von Ausreißern abmildern. Gelegentlich gibt es in einem Datensatz einige wenige Beobachtungen, die mit geringer Wahrscheinlichkeit aus dem Schwanz ihrer Verteilungen entnommen wurden, oder es gibt einige wenige Beobachtungen, die aus Verteilungen entnommen wurden, die geringfügig von der bei der Schätzung der kleinsten Quadrate verwendeten Normalitätsannahme abweichen und somit den Datensatz verunreinigen. Diese abweichenden Beobachtungen, die als Ausreißer in der Antwortvariablen bezeichnet werden, können sich erheblich auf die Anpassungsergebnisse auswirken, da sie relativ große (rohe oder gewichtete) Residuen aufweisen und somit die Summe der Quadrate, die minimiert werden soll, aufblähen.
Eine Möglichkeit, die Auswirkungen von Ausreißern abzuschwächen, ist die Verwendung einer Gewichtungsvariablen, die eine Funktion der Residuen (und damit auch eine Funktion der Parameter) ist, wobei das einer Beobachtung zugewiesene Gewicht umgekehrt zur Größe des Residuums steht. Die Definition der zu verwendenden Gewichtungsfunktion hängt von den Annahmen über die Verteilungen der Beobachtungen (unter der Annahme, dass sie nicht normal sind) und einem Schema für die Entscheidung ab, welche Größe der Residuen zu tolerieren ist. Die Cauchy-Gewichtungsfunktion ist durch die Residuen y-f definiert, wobei y der Wert der abhängigen Variable und f die Anpassungsfunktion ist, und kann zur Minimierung der Auswirkungen von Ausreißern verwendet werden.
Gewicht_Cauchy = 1/(1+4*(y-f)^2)
Der Algorithmus zur Parameterschätzung, den wir für die adaptive Gewichtung verwenden, iterativ neu gewichtete kleinste Quadrate (IRLS), basiert auf der Lösung einer Folge von Problemen mit konstanter Gewichtung der kleinsten Quadrate, wobei jedes Teilproblem mit unserer aktuellen Implementierung des Levenberg-Marquardt-Algorithmus gelöst wird. Dieser Prozess beginnt mit der Bewertung der Gewichte unter Verwendung der anfänglichen Parameterwerte und der anschließenden Minimierung der Summe der Quadrate mit diesen festen Gewichten. Die am besten passenden Parameter werden dann zur Neubewertung der Gewichte verwendet.
Mit den neuen Gewichtswerten wird das oben beschriebene Verfahren zur Minimierung der Summe der Quadrate wiederholt. Wir fahren auf diese Weise fort, bis Konvergenz erreicht ist. Das Kriterium für die Konvergenz ist, dass der relative Fehler zwischen der Quadratwurzel der Summe der gewichteten Residuen für die aktuellen Parameterwerte und der Quadratwurzel der Summe der gewichteten Residuen für die Parameterwerte der vorherigen Iteration kleiner ist als der in der Gleichung festgelegte Toleranzwert. Wie bei anderen Schätzverfahren auch, ist die Konvergenz nicht garantiert.
