Grafiti LLC
Confidence Bands
Confidence Intervals & Confidence Bands
Basics
Sometimes we are asked how to get confidence intervals in linear models in Grafiti. It is actually not very hard and, here, we shall review the technique. Before we do, however, let’s review the basic ideas behind a confidence interval for a linear model.
First, if we have a linear regression of Y on the variable X, then we are actually saying that, for a given value of X, the value of Y is given by Y=aX+b+e where e is a “noise term.”
The noise term is usually assumed to be normally distributed with a mean of 0 and a variance of s^2. The trick for a real data set is to estimate a and b and then to carry out inferences on those estimates using an estimated value of s^2.
Sometimes, however, we would like to find a confidence interval for the mean of Y at a specified value of X. According to the equation above, the mean of Y at X is aX+b.
However, in a real data set, we never know the “true” values of a and b; all we know are our estimates. Therefore, it is appropriate to find an interval in which we can be relatively confident the true mean of Y occurs.
There are some very messy formulae for calculating this interval but we shall not go into them here. After all, the computer should make the computation easy. So, suppose we take the sample data set USSTATES.SYD, with 48 valid cases for the variables CARDIO and CANCER. Use the Statistics > Regression > Linear dialog box to set up the regression model or issue the commands:
REGRESS
USE usstates
SAVE regress/MODEL
MODEL cancer=CONSTANT+cardio
ESTIMATE
The computer will then estimate the model, finding estimated values for both the constant and the coefficient of CARDIO and printing out an analysis of variance table.
In this instance it will also save a file, REGRESS.SYD, that contains the residuals from the model, estimates of CANCER based on CARDIO for the model (the variable named ESTIMATE) and a mysterious value called SEPRED. It is SEPRED that we will use to calculate our confidence intervals.
SEPRED stands for “Standard Error of the Predicted Value. The file will also have the values of the original data. These are saved because we added the MODEL option to the SAVE command.
To calculate the UPPER and LOWER limits of a 95% confidence interval for the predicted values of CANCER, use the Data > Transform > Let dialog box or enter the BASIC module and issue the commands:
BASIC
USE regress
LET n=48
LET nvars=2
LET upper = estimate+TIF(.975,n-nvars)*sepred
LET lower = estimate-TIF(.975,n-nvars)*sepred
PRINT upper lower
RUN
The UPPER and LOWER confidence limits for the estimated value of CANCER for each case will then be printed out. In the above, TIF stands for the “Inverse t-distribution.”
The above ideas can be generalized in several different ways. For example, if you wish to find a confidence interval for the mean of Y for a regression on two variables, you only need to add those variables to the MODEL statement in REGRESS and change NVARS from 2 to 3 in the BASIC module. (Note: N-NVARS represents the number of valid cases minus the number of variables in the model. Set N and NVARS above to the correct number of cases and variables for your model.
Confidence Intervals for the Mean of Y at New Values of X
It may happen that you wish to find the confidence interval for the mean of Y at one or more new values of your X variable. Put the new values of X at the end of your file and make the associated Y values zero. (You don’t need to worry about what the Y-value actually is. This Y-value is just a placeholder and will not enter into the calculations.)
Next, add a new variable in your file called WT. WT should have the value 1 for the cases on which you have data for both X and Y, and 0 for the cases with new values of X. After saving the file, use the Data > Frequency dialog to select WT as your weighting variable, or issue the command:
FREQUENCY=WT
Using the Statistics > Regression > Linear dialog box or a command file, estimate your regression model again, remembering to save the results to a data file with MODEL option. The FREQUENCY command is very useful in this context; in calculating the regression, points with weight 1 will be used once, points with weight zero will be used zero times.
Thus, the regression will be calculated for the cases with known values of Y and X. However, the value of ESTIMATE will be calculated for all cases. Using the file of saved results, you can use the calculation above to derive the confidence interval for the estimated mean of an unknown Y at a known value of X for the new cases.
Subtleties
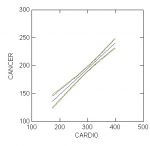 When you plot the confidence intervals for the estimated values of CANCER and the confidence bands for the regression line, you’ll see that the confidence band is wider than the confidence interval:
BEGIN
PLOT cancer*x(1) / SIZE=0 SMOOTH=LINEAR SHORT YMIN=100 YMAX=300 ,
XMIN=100 XMAX=500 XLABEL=’CARDIO’ COLOR=BLUE
PLOT upper,lower*x(1) /SIZE=0 SMOOTH=SPLINE SHORT YMIN=100,
YMAX=300 XMIN=100 XMAX=500 YLABEL=’ ‘,
XLABEL=’ ‘ COLOR=RED OVERLAY
PLOT upperband,lowerband*x(1) /SIZE=0 SMOOTH=SPLINE SHORT,
YMIN=100 YMAX=300 XMIN=100 XMAX=500 YLABEL=’ ‘,
XLABEL=’ ‘ COLOR=GREEN OVERLAY
END
When you plot the confidence intervals for the estimated values of CANCER and the confidence bands for the regression line, you’ll see that the confidence band is wider than the confidence interval:
BEGIN
PLOT cancer*x(1) / SIZE=0 SMOOTH=LINEAR SHORT YMIN=100 YMAX=300 ,
XMIN=100 XMAX=500 XLABEL=’CARDIO’ COLOR=BLUE
PLOT upper,lower*x(1) /SIZE=0 SMOOTH=SPLINE SHORT YMIN=100,
YMAX=300 XMIN=100 XMAX=500 YLABEL=’ ‘,
XLABEL=’ ‘ COLOR=RED OVERLAY
PLOT upperband,lowerband*x(1) /SIZE=0 SMOOTH=SPLINE SHORT,
YMIN=100 YMAX=300 XMIN=100 XMAX=500 YLABEL=’ ‘,
XLABEL=’ ‘ COLOR=GREEN OVERLAY
END
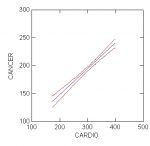
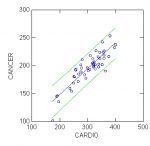 BEGIN
PLOT cancer*x(1) /SMOOTH=LINEAR SHORT YMIN=100 YMAX=300 XMIN=100,
XMAX=500 XLABEL=’CARDIO’ COLOR=BLUE
PLOT upperband,lowerband*x(1) / SIZE=0 SMOOTH=SPLINE SHORT,
YMIN=100 YMAX=300 XMIN=100 XMAX=500 YLABEL=’ ‘,
XLABEL=’ ‘ COLOR=GREEN OVERLAY
END
This will plot the confidence bands or prediction intervals around the data.
BEGIN
PLOT cancer*x(1) /SMOOTH=LINEAR SHORT YMIN=100 YMAX=300 XMIN=100,
XMAX=500 XLABEL=’CARDIO’ COLOR=BLUE
PLOT upperband,lowerband*x(1) / SIZE=0 SMOOTH=SPLINE SHORT,
YMIN=100 YMAX=300 XMIN=100 XMAX=500 YLABEL=’ ‘,
XLABEL=’ ‘ COLOR=GREEN OVERLAY
END
This will plot the confidence bands or prediction intervals around the data.
