sigmaplot-product-features

INPIXON

Características del producto SigmaPlot

Nuevas funciones y mejoras en SigmaPlot

Parcelas forestales
Gráficos de densidad del núcleo
10 nuevas combinaciones de colores
Gráfico de densidad de puntos con barras de error medio y estándar
Leyenda Mejoras
- Leyendas horizontales, verticales y rectangulares
  - Cursor sobre lateral o asa superior o inferior
- - permite leyendas de varias columnas
- Interfaz de usuario para establecer el número de columnas de elementos de leyenda en el cuadro de diálogo Propiedades. Los números de columna permitidos se muestran en la lista combinada
- Cambie el número de columnas de la leyenda seleccionando y arrastrando el asa central del cuadro delimitador.
- Reordenar los elementos de la leyenda
  - A través del cuadro de diálogo de propiedades: desplace uno o varios elementos de la leyenda hacia arriba o hacia abajo mediante el control arriba/abajo situado en la parte superior del cuadro de lista.
  - Mediante el movimiento del cursor: desplaza uno o varios elementos de la leyenda hacia arriba o hacia abajo. Seleccione el elemento o elementos de la leyenda y utilice las flechas arriba y abajo del teclado para desplazarse por el cuadro delimitador.
  - Mediante la selección con el ratón y el movimiento del cursor de los elementos del cuadro delimitador
- Ajustes de las propiedades de los elementos individuales de la leyenda: seleccione elementos individuales de la leyenda y utilice la minibarra de herramientas para cambiar las propiedades.
  - Control de la región en blanco del cuadro de leyenda mediante el cursor
  - Cursor sobre asa de esquina
  - permite un redimensionamiento proporcional
- Añadir etiquetado directo sencillo
  - Admite «Etiquetado directo» en el cuadro de diálogo de propiedades mediante el control de casilla de verificación «Etiquetado directo».
  - Desagrupar los elementos de la leyenda: los elementos individuales de la leyenda pueden desplazarse a las ubicaciones preferidas y moverse junto con el gráfico.
- Se ha añadido soporte para Leyenda Título (sin título por defecto). El usuario puede añadir un título al cuadro de leyenda utilizando el panel de propiedades de la leyenda
- Invertir los elementos de la leyenda mediante el menú contextual del botón derecho del ratón
- Para abrir las Propiedades de la Leyenda, haga doble clic en Leyenda Sólida o Leyenda Texto.
- Se ha añadido Restablecer a las leyendas para restablecer las opciones de leyenda a los valores predeterminados.

Nuevas funciones de análisis

Análisis de componentes principales (ACP)
Análisis de covarianza (ANCOVA)
Añadidos valores P a comparaciones múltiples para ANOVAs no paramétricos.
Se han eliminado las opciones del cuadro combinado para los niveles de significación de las comparaciones múltiples y se ha vinculado el nivel de significación de las comparaciones múltiples a la prueba principal (general).
Se ha añadido el criterio de información de Akaike a los informes del Asistente de regresión y del Asistente de ajuste dinámico y al cuadro de diálogo Opciones de informe.
Se ha vuelto a añadir el botón Reejecutar en el grupo SigmaStat.
Actualizada la biblioteca de ajuste standard.jfl
- Se han añadido funciones de probabilidad, que ahora incluyen 24, para el ajuste de curvas o la visualización de funciones.
- El valor de tolerancia de todas las ecuaciones se ha modificado para utilizar «e-notación» en lugar de decimal fijo. Esto permite al usuario leer el valor sin desplazarse.
- Añadir siete funciones de ponderación a todas las ecuaciones de ajuste de curvas en standard.jfl. Se ha añadido una ligera variante para las ecuaciones 3D.

Nuevas funciones de la interfaz de usuario

Reorganizar los elementos de Notebook en una sección arrastrándolos
Nuevo tutorial SigmaPlot en PDF
Anchos de línea de una columna de la hoja de cálculo

Nuevas funciones de importación y exportación

Se han añadido los formatos de archivo SVG y SWF para la exportación de gráficos vectoriales escalables.
Se ha añadido la exportación de PDF vectorial para mejorar el PDF rasterizado existente.
Se añade compatibilidad con la importación y exportación de archivos para las versiones 13 y 14 de Minitab, la versión 9 de SAS, la versión 19 de SPSS y la versión 13 de Symphony.

Características del producto SigmaPlot

Parcela forestal

Un diagrama de bosque es una forma de "metaanálisis" que se utiliza para combinar múltiples análisis que abordan la misma cuestión. El metanálisis combina estadísticamente las muestras de cada estudio contribuyente para crear una estadística de resumen global que es más precisa que el tamaño del efecto en los estudios individuales. Los valores individuales de los estudios y sus intervalos de confianza del 95% se muestran como símbolos cuadrados con barras de error horizontales y la estadística de resumen global como un rombo con una anchura igual a su intervalo de confianza del 95%.

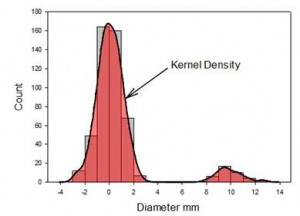
Densidad del núcleo

La función de densidad del núcleo generará una estimación de la distribución de datos subyacente. Esto debe compararse con el histograma escalonado. Tiene ventajas (ausencia de barras) y desventajas (pérdida de información de recuento) con respecto a un histograma y debe utilizarse junto con éste. Pueden crearse simultáneamente.

Densidad de puntos con barras de error medio y estándar

Se ha añadido al gráfico Densidad de puntos el cálculo de la media más barras de error estándar, símbolo más barras de error. Esto mejora las otras estadísticas posibles de visualización de densidad de puntos: media, mediana, percentiles y boxplot.

Nuevas combinaciones de colores

Se han implementado diez nuevas combinaciones de colores. A continuación se muestran tres ejemplos:

Leyenda Mejoras - Formas

Ahora hay disponibles leyendas verticales, horizontales y rectangulares.

Orden inverso de la leyenda

Ahora puede seleccionar invertir el orden de los elementos de la leyenda. Esto proporciona un orden más lógico para algunos tipos de gráficos.

Reordenar elementos de leyenda

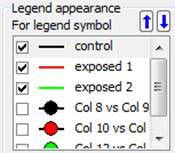
Hay tres formas de reordenar los elementos de la leyenda. Como se muestra aquí, puede mover uno o varios elementos de leyenda hacia arriba o hacia abajo utilizando los controles de flecha arriba/abajo del panel Leyendas de Propiedades de Gráfico. Aún más fácil, sólo tienes que seleccionar el elemento en la leyenda y utilizar las teclas de flecha arriba y abajo del teclado. O seleccione el elemento de la leyenda y arrástrelo a la nueva posición con el cursor del ratón.

Edición de elementos de leyenda en la minibarra de herramientas

Los elementos de leyenda pueden editarse ahora haciendo clic en el elemento y utilizando la minibarra de herramientas.

Etiquetado directo

Ahora es posible desagrupar la leyenda y colocar elementos individuales de leyenda junto a las parcelas correspondientes. Las etiquetas se moverán con el gráfico para mantener la posición con respecto a éste. Como la etiqueta está junto a la parcela, la identificación visual de cada parcela es ahora mucho más fácil.

Análisis de componentes principales (ACP)

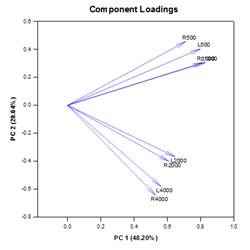
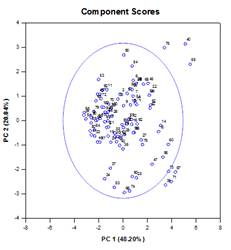
El análisis de componentes principales (ACP) es una técnica para reducir la complejidad de los datos de alta dimensión mediante la aproximación de los datos con menos dimensiones. Cada nueva dimensión se denomina componente principal y representa una combinación lineal de las variables originales. El primer componente principal tiene en cuenta la mayor variación posible de los datos. Cada componente principal subsiguiente explica la mayor parte posible de la variación restante y es ortogonal a todos los componentes principales anteriores.

Puede examinar los componentes principales para comprender las fuentes de variación de sus datos. También puede utilizarlos para formar modelos predictivos. Si la mayor parte de la variación de los datos se encuentra en un subconjunto de baja dimensión, es posible que pueda modelizar la variable de respuesta en términos de componentes principales. Puede utilizar componentes principales para reducir el número de variables en regresión, agrupación y otras técnicas estadísticas.

El resultado gráfico consiste en gráficos de Scree, Cargas de Componentes y Puntuaciones de Componentes.

Análisis de covarianza (ANCOVA)

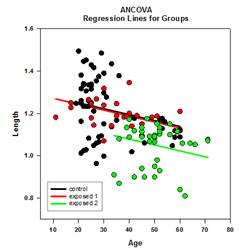
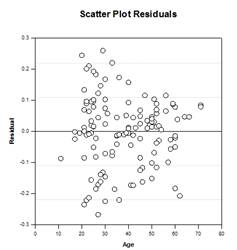
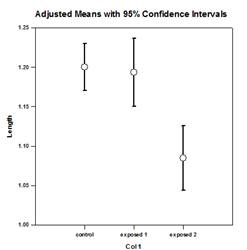
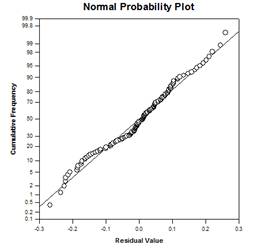
Un modelo ANOVA de un solo factor se basa en un diseño completamente aleatorizado en el que los sujetos de un estudio se seleccionan aleatoriamente de una población y luego cada sujeto se asigna aleatoriamente a uno de varios niveles de factor o tratamientos, de modo que cada sujeto tiene la misma probabilidad de recibir un tratamiento. Un supuesto común de este diseño es que los sujetos son homogéneos. Esto significa que cualquier otra variable, cuando existen diferencias entre los sujetos, no altera significativamente el efecto del tratamiento y no es necesario incluirla en el modelo. Sin embargo, a menudo hay variables, fuera del control del investigador, que afectan a las observaciones dentro de uno o más grupos de factores, lo que da lugar a ajustes necesarios en las medias de los grupos, sus errores, las fuentes de variabilidad y los valores P del efecto de grupo, incluidas las comparaciones múltiples.

Estas variables se denominan covariables. Suelen ser variables continuas, pero también pueden ser categóricas. Dado que suelen tener una importancia secundaria para el estudio y, como ya se ha dicho, no pueden ser controlados por el investigador, no representan factores adicionales de los efectos principales, pero pueden incluirse en el modelo para mejorar la precisión de los resultados. Las covariables también se conocen como variables molestas o variables concomitantes.

ANCOVA (Análisis de Covarianza) es una extensión de ANOVA que se obtiene especificando una o más covariables como variables adicionales en el modelo. Si organiza los datos ANCOVA en una hoja de trabajo de SigmaPlot utilizando el formato de datos indexados, una columna representará el factor y una columna representará la variable dependiente (las observaciones) como en un diseño ANOVA. Además, tendrá una columna para cada covariable. Cuando se utiliza un modelo que incluye los efectos de las covariables, hay más variabilidad explicada en el valor de la variable dependiente.

En general, esto reduce la varianza no explicada que se atribuye a la variabilidad aleatoria del muestreo, lo que aumenta la sensibilidad del ANCOVA en comparación con el mismo modelo sin covariables (el modelo ANOVA). Una mayor sensibilidad de la prueba significa que las diferencias medias más pequeñas entre tratamientos serán significativas en comparación con un modelo ANOVA estándar, lo que aumenta la potencia estadística.

Como ejemplo sencillo de uso de ANCOVA, considere un experimento en el que los alumnos son asignados aleatoriamente a uno de tres tipos de métodos de enseñanza y se miden sus puntuaciones de rendimiento. El objetivo es medir el efecto de los distintos métodos y determinar si uno de ellos consigue una puntuación media significativamente más alta que los demás. Los métodos son la clase magistral, el autoaprendizaje y el aprendizaje cooperativo. Si se realiza un ANOVA de una vía con estos datos hipotéticos, se obtienen los resultados de la tabla siguiente, bajo el encabezamiento de la columna ANOVA. Llegamos a la conclusión de que no hay diferencias significativas entre los métodos de enseñanza. Obsérvese también que la varianza no explicada por el modelo ANOVA que se debe a la variabilidad aleatoria del muestreo en las observaciones se estima en 35,17.

Es posible que los estudiantes de nuestro estudio se beneficien más de un método que de los otros, en función de su rendimiento académico previo. Supongamos que refinamos el estudio para incluir una covariable que mida alguna capacidad previa, como una Evaluación Basada en Estándares (SBA) sancionada por el estado. Si se realiza un ANCOVA de una vía con estos datos, se obtienen los resultados de la tabla siguiente, bajo el encabezamiento de la columna ANCOVA.

La media ajustada que figura en la tabla para cada método es una corrección de la media del grupo para controlar los efectos de la covariable. Los resultados muestran que las medias ajustadas son significativamente diferentes, siendo el método Lecture el más exitoso. Observe cómo los errores estándar de las medias han disminuido en casi un factor de tres, mientras que la varianza debida a la variabilidad aleatoria de la muestra ha disminuido en un factor de diez. Una reducción del error es la consecuencia habitual de introducir covariables y realizar un análisis ANCOVA.

Hay cuatro gráficos de resultados ANCOVA - Líneas de Regresión en Grupos, Diagrama de Dispersión de Residuales, Medias Ajustadas con Intervalos de Confianza y Diagrama de Probabilidad de Normalidad:

Valores P para ANOVA no paramétricos

Las pruebas no paramétricas de ANOVA en SigmaPlot son la prueba de Kruskal-Wallis (ANOVA unidireccional en rangos) y la prueba de Friedman (ANOVA unidireccional de medidas repetidas en rangos). Ambos proporcionan cuatro procedimientos de pruebas post hoc para determinar el origen de los efectos significativos en el factor de tratamiento. Los cuatro procedimientos son Tukey, SNK, de Dunn y de Dunnett.

Los tres primeros procedimientos pueden utilizarse para comprobar la significación de cada comparación por pares de los grupos de tratamiento, mientras que los dos últimos pueden utilizarse para comprobar la significación de las comparaciones con un grupo de control. El método de Dunn es el único procedimiento disponible si los grupos de tratamiento tienen tamaños de muestra desiguales.

Cuando se utiliza un procedimiento de prueba post hoc, se incluye en el informe una tabla con los resultados de las comparaciones por pares de los niveles de tratamiento. La última columna de la tabla muestra si la diferencia de rango es significativa o no. En versiones anteriores de SigmaPlot no se proporciona un valor p ajustado que pueda compararse con el nivel de significación del ANOVA (normalmente 0,05) para determinar la significación.

Esto se debe a que SigmaPlot ha estado determinando la significación comparando el estadístico de prueba observado, calculado para cada comparación, con un valor crítico de la distribución del estadístico que se obtiene de una tabla de consulta. SigmaPlot tenía dos conjuntos de tablas de consulta para las distribuciones de probabilidad correspondientes a los cuatro métodos post-hoc, donde un conjunto era para un nivel de significación de 0,05 y otro conjunto era para un nivel de significación de 0,01.

Esto se ha cambiado recientemente para utilizar procedimientos analíticos para calcular los valores p de estas distribuciones, con lo que las tablas de consulta han quedado obsoletas. Gracias a este cambio, ahora podemos informar de los valores p ajustados para cada comparación por pares. Este cambio también permite eliminar la restricción de utilizar 0,05 y 0,01 como únicos niveles de significación para las comparaciones múltiples. Así, el usuario puede introducir cualquier nivel de significación de valor P válido de 0 a 1.

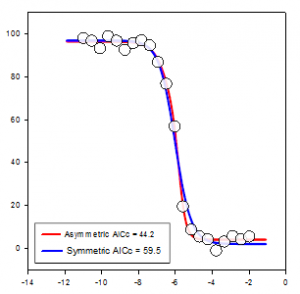
Criterio de información de Akaike (AICc)

El criterio de información de Akaike (AIC) proporciona un método para medir el rendimiento relativo en el ajuste de un modelo de regresión a un conjunto dado de datos. Basado en el concepto de entropía de la información, el criterio ofrece una medida relativa de la información que se pierde al utilizar un modelo para describir los datos. Más concretamente, ofrece un compromiso entre maximizar la verosimilitud del modelo estimado (lo mismo que minimizar la suma de cuadrados residual si los datos se distribuyen normalmente) y mantener al mínimo el número de parámetros libres del modelo, reduciendo su complejidad. Aunque la bondad del ajuste casi siempre mejora añadiendo más parámetros, un ajuste excesivo aumentará la sensibilidad del modelo a los cambios en los datos de entrada y puede arruinar su capacidad de predicción.

La razón básica para utilizar el AIC es como guía para la selección de modelos. En la práctica, se calcula para un conjunto de modelos candidatos y un conjunto de datos determinado. El modelo con el valor AIC más bajo se selecciona como el modelo del conjunto que mejor representa el modelo "verdadero", o el modelo que minimiza la pérdida de información, que es lo que el AIC está diseñado para estimar. Una vez determinado el modelo con el AIC mínimo, también se puede calcular una probabilidad relativa para cada uno de los otros modelos candidatos para medir la probabilidad de reducir la pérdida de información en relación con el modelo con el AIC mínimo. La probabilidad relativa puede ayudar al investigador a decidir si debe conservar más de un modelo del conjunto para seguir estudiándolo.

El cálculo del AIC se basa en la siguiente fórmula general obtenida por Akaike

dondees el número de parámetros estimables en el problema de regresión, que incluye los parámetros del modelo y la varianza desconocida de las observaciones, y es el valor maximizado de la función de verosimilitud para el modelo estimado.

Cuando el tamaño de la muestra de los datos es pequeño en relación con el número de parámetros (algunos autores dicen que cuando no es más que unas pocas veces mayor que), el AIC no funcionará tan bien para proteger contra el sobreajuste. En este caso, existe una versión corregida del AIC dada por

Se observa que el AICc impone una penalización mayor que el AIC cuando hay parámetros adicionales. La mayoría de los autores parecen estar de acuerdo en que debe utilizarse AICc en lugar de AIC en todas las situaciones y es AICc lo que se implementa en SigmaPlot. La ecuación asimétrica del gráfico es significativamente mejor que la simétrica, ya que su valor AICc es más de 7 unidades inferior al de la ecuación simétrica, una regla empírica para el AICc. Si la diferencia es superior a 2, la ecuación con el valor AICc más pequeño no debe considerarse la mejor, sino una candidata a mejor ecuación.

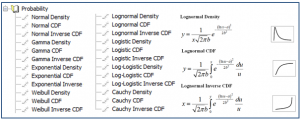
Funciones de probabilidad de regresión no lineal

Se han añadido 24 nuevas funciones de ajuste probabilístico a la biblioteca de ajuste standard.jfl. A continuación se muestran estas funciones y algunas ecuaciones y formas gráficas.

Funciones de ponderación de regresión no lineal

Ahora hay siete funciones de ponderación diferentes incorporadas en cada ecuación de regresión no lineal (las 3D son ligeramente diferentes). Estas funciones son y recíproca, y recíproca al cuadrado, x recíproca, x recíproca al cuadrado, predicteds recíproca, predicteds recíproca al cuadrado y Cauchy. El algoritmo de mínimos cuadrados reponderados iterativamente se utiliza para permitir que las ponderaciones cambien durante cada iteración de regresión no lineal. De este modo, la "ponderación por predicados", un método comúnmente utilizado, puede obtenerse seleccionando la opción de ponderación reciprocal_pred.

Además, la ponderación Cauchy (seleccione weight_Cauchy) se puede utilizar para ajustar una ecuación a datos que contienen valores atípicos y el efecto de los valores atípicos se reducirá al mínimo. Los usuarios pueden crear sus propios métodos de ponderación en términos de residuos y/o parámetros para aplicar otros métodos de ajuste robustos. La sección de ecuaciones de un archivo de ajuste se muestra con las siete funciones de ponderación incorporadas.

Características de la interfaz de usuario - Reorganiza los elementos de tu bloc de notas arrastrándolos

Los objetos de una sección de cuaderno no se crean necesariamente en un orden lógico. Ahora puede arrastrar elementos dentro de una sección a nuevas posiciones para colocarlos de forma más lógica.

Tutorial actualizado de SigmaPlot

El nuevo tutorial facilita la creación de gráficos por primera vez. Empieza con ejemplos sencillos y poco a poco se va haciendo más complejo.

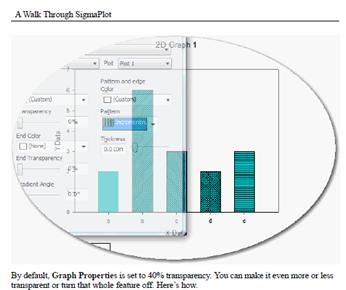
Especificar anchos de línea de trazado desde una columna de hoja de cálculo

Ahora es posible introducir valores de anchura de línea en una columna de la hoja de cálculo. Estos valores pueden utilizarse dentro de un gráfico o en varios gráficos de la página.

Nuevos formatos de archivos vectoriales de exportación

Se han añadido los formatos de archivo SVG (Scalable Vector Graphics), SWF (Adobe Flash Player) y PDF vectorial. Se trata de formatos escalables en los que no se pierde resolución al hacer zoom a distintos niveles. SVG es el formato gráfico estándar para la web y SWF puede utilizarse con Adobe Flash Player. Dado que el formato PDF se utiliza con tanta frecuencia, el formato PDF vectorial está ahora asociado al botón Crear PDF de la cinta Inicio.

Formatos de solicitud actualizados

Se ha actualizado la compatibilidad con la importación y exportación de archivos a las versiones 13 y 14 de Minitab, la versión 9 de SAS y la versión 19 de SPSS.