Caractéristiques générales
Nouvelles fonctionnalités
En 2007, les fonctions et caractéristiques de SigmaStat ont été intégrées dans SigmaPlot à partir de la version 11. Cependant, le 1er février 2016, SigmaStat 4.0 a été publié et est maintenant disponible en tant que produit autonome.
Vous trouverez ci-dessous les nombreuses améliorations apportées aux fonctions d'analyse statistique de SigmaStat :
- Analyse en composantes principales (ACP) - L'analyse en composantes principales est une technique qui permet de réduire la complexité des données à haute dimension en les approximant avec moins de dimensions.
- Analyse de la covariance (ANCOVA) - L'analyse de la covariance est une extension de l'ANOVA (analyse de la variance) obtenue en spécifiant une ou plusieurs covariables comme variables supplémentaires dans le modèle.
- Régression de Cox - Elle comprend le modèle des risques proportionnels avec stratification pour étudier l'impact des facteurs de risque potentiels sur la durée de survie d'une population. Les données d'entrée peuvent être catégoriques.
- Test T à un échantillon - Teste l'hypothèse selon laquelle la moyenne d'une population est égale à une valeur spécifiée.
- Tests du rapport de cotes et du risque relatif - Ces deux tests vérifient l'hypothèse selon laquelle un traitement n'a pas d'effet sur le taux d'occurrence d'un événement donné dans une population. Le rapport de cotes est utilisé dans les études rétrospectives pour déterminer l'effet du traitement après l'observation de l'événement. Le risque relatif est utilisé dans les études prospectives où les groupes de traitement et de contrôle ont été choisis avant que l'événement ne se produise.
- Test de normalité de Shapiro-Wilk - Test plus précis que celui de Kolmogorov-Smirnov pour évaluer la normalité des données échantillonnées. Utilisé dans la vérification des hypothèses pour de nombreux tests statistiques, mais peut également être utilisé directement sur les données de la feuille de calcul.
- Nouveau graphique de résultats - ANOVA Profile Plots : Utilisé pour analyser les effets principaux et les interactions d'ordre supérieur des facteurs dans un plan ANOVA multifactoriel en comparant les moyennes des moindres carrés.
- Nouvelles transformations de probabilités - Trente-quatre nouvelles fonctions ont été ajoutées au langage de transformation de SigmaStat pour calculer les probabilités et les scores associés aux distributions qui apparaissent dans de nombreux domaines d'étude.
- Nouveau changement d'interface - Régression non linéaire : Une interface d'assistant facile à utiliser et des rapports plus détaillés.
- Nouveau changement d'interface - Transformations rapides : Une façon plus simple d'effectuer des calculs dans la feuille de calcul.
- Nouveau changement d'interface - Nouvelle interface utilisateur : Permet à l'utilisateur de travailler plus facilement avec les feuilles de calcul Excel.
- Correction de Yates ajoutée au test de Mann-Whitney - La correction de Yates pour la continuité, ou test chi-carré de Yates, est utilisée pour tester l'indépendance dans un tableau de contingence afin d'évaluer si deux échantillons d'observations proviennent de la même distribution.
- Messages d'erreur améliorés - Les messages d'erreur améliorés ajoutent des informations lorsque la vérification des hypothèses pour l'ANOVA a échoué.
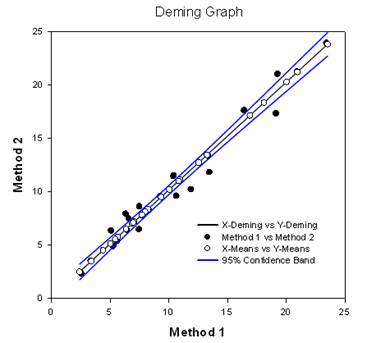
- Régression de Deming - La régression de Deming permet de tenir compte des erreurs dans les variables X et Y. Il s'agit d'une technique de comparaison des méthodes où les données X proviennent d'une méthode et les données Y de l'autre. La méthode de régression de Deming étend fondamentalement la régression linéaire normale, où les valeurs X sont considérées comme exemptes d'erreur, au cas où X et Y (les deux méthodes) comportent une erreur. Des hypothèses peuvent ensuite être testées, une pente différente de celle de 1.0 par exemple, pour déterminer si les méthodes sont les mêmes. Par exemple, elle peut être utilisée pour comparer deux instruments conçus pour mesurer la même substance ou pour comparer deux méthodes algorithmiques de détection de tumeurs dans des images. Le graphique compare les deux méthodes pour déterminer si elles sont différentes ou identiques. Un rapport donne des résultats statistiques.
- Critère d'information d'Akaike (AICc) - Le critère d'information d'Akaike est désormais disponible dans les rapports de régression non linéaire. Il s'agit d'un critère de qualité d'ajustement qui tient également compte du nombre de paramètres dans l'équation. Elle est également valable pour les équations non imbriquées que l'on rencontre, par exemple, dans les analyses de cinétique enzymatique.
- Nouvelles fonctions de probabilité pour la régression non linéaire - Au total, 24 fonctions de probabilité ont été ajoutées à la bibliothèque d'ajustement des courbes. Des équations automatiques d'estimation des paramètres initiaux ont été créées pour chacun d'entre eux.
- Pondération de la régression non linéaire - Il existe désormais sept fonctions de pondération différentes intégrées dans chaque équation de régression non linéaire (les 3D sont légèrement différentes). Ces fonctions sont les suivantes : y réciproque, y réciproque au carré, x réciproque, x réciproque au carré, prédictions réciproques, prédictions réciproques au carré et Cauchy. L'algorithme des moindres carrés repondérés de manière itérative est utilisé pour permettre aux poids de changer au cours de chaque itération de régression non linéaire.
- Amélioration des tests de comparaisons multiples - Deux améliorations importantes ont été apportées. Les valeurs P pour les résultats de l'ANOVA non paramétrique ont été ajoutées. Ceux-ci n'existaient pas auparavant. De même, les valeurs P des comparaisons multiples ont été limitées à des choix discrets (0,05, 0,01, etc.). Cette limitation n'existe plus et toute valeur P valide peut être utilisée.
Nouveaux tests statistiques majeurs
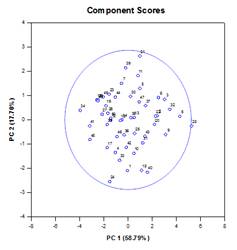
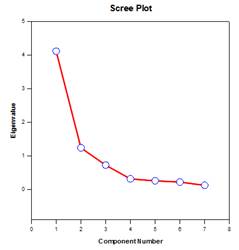
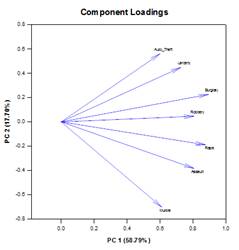
Analyse en composantes principales (ACP) – L’analyse en composantes principales est une technique qui permet de réduire la complexité des données à haute dimension en les approximant avec moins de dimensions. Chaque nouvelle dimension est appelée composante principale et représente une combinaison linéaire des variables originales. La première composante principale tient compte de la plus grande variation possible des données. Chaque composante principale suivante rend compte de la plus grande partie possible de la variation restante et est orthogonale à toutes les composantes principales précédentes.
Vous pouvez examiner les composantes principales pour comprendre les sources de variation de vos données. Vous pouvez également les utiliser pour élaborer des modèles prédictifs. Si la plupart des variations de vos données existent dans un sous-ensemble à faible dimension, vous pouvez peut-être modéliser votre variable de réponse en termes de composantes principales. Vous pouvez utiliser les composantes principales pour réduire le nombre de variables dans la régression, le regroupement et d’autres techniques statistiques. L’objectif principal de l’analyse en composantes principales est d’expliquer les sources de variabilité des données et de représenter les données avec moins de variables tout en préservant la majeure partie de la variance totale.
Exemples de graphiques des composantes principales :
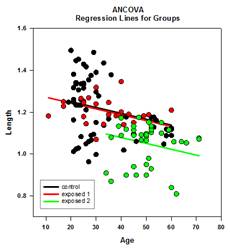
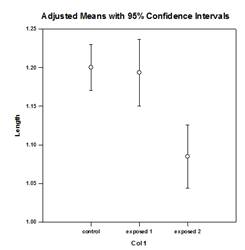
Analyse de covariance (ANCOVA) – L’analyse de covariance est une extension de l’ANOVA obtenue en spécifiant une ou plusieurs covariables comme variables supplémentaires dans le modèle. Si vous organisez les données ANCOVA dans une feuille de calcul SigmaPlot en utilisant le format de données indexées, une colonne représentera le facteur et une colonne représentera la variable dépendante (les observations) comme dans un plan ANOVA. En outre, vous aurez une colonne pour chaque covariable.
Exemples de graphiques ANCOVA :
Nouvelles caractéristiques statistiques
Amélioration des comparaisons multiples – Une amélioration significative a été apportée au calcul de la valeur P des comparaisons multiples. Les procédures de comparaison multiple suivantes, Tukey (tests non paramétriques), SNK (tests non paramétriques), Dunnett, Dunn (uniquement non paramétriques) et Duncan ne calculent pas les valeurs p de manière analytique, mais utilisent des tables de recherche des valeurs critiques pour une distribution particulière afin de déterminer, par interpolation si nécessaire, si une statistique de test calculée représente une différence significative entre les moyennes des groupes. Par conséquent, les valeurs p n’ont pas été rapportées pour ces tests, mais seulement la conclusion sur l’existence ou non d’une différence significative. Le problème majeur de cette approche est que les tables de recherche ne sont disponibles que pour deux niveaux de signification, 0,05 et 0,01. Un autre problème est que de nombreux clients souhaitent connaître les valeurs p. Pour SigmaPlot, des algorithmes ont été codés pour calculer les distributions des statistiques de test pour toutes les procédures post-hoc, ce qui rend les tables de recherche obsolètes. En conséquence, les valeurs p ajustées pour toutes les procédures post-hoc sont désormais incluses dans le rapport. En outre, il n’est plus nécessaire de limiter le niveau de signification des comparaisons multiples à 0,05 ou 0,01. Au lieu de cela, le niveau de signification des comparaisons multiples sera le même que le niveau de signification du test principal (omnibus). Il n’y a pas de limite à cette valeur p – toute valeur valide peut être utilisée.
Critère d’information d’Akaike (AICc ) – Le critère d’information d’Akaike a été ajouté aux rapports de l’assistant de régression et de l’assistant d’ajustement dynamique ainsi qu’à la boîte de dialogue Options de rapport. Il fournit une méthode pour mesurer la performance relative de l’ajustement d’un modèle de régression à un ensemble donné de données. Fondé sur le concept d’entropie de l’information, le critère offre une mesure relative de l’information perdue lors de l’utilisation d’un modèle pour décrire les données.
Plus précisément, il s’agit d’un compromis entre la maximisation de la vraisemblance du modèle estimé (ce qui revient à minimiser la somme des carrés résiduels si les données sont normalement distribuées) et le maintien au minimum du nombre de paramètres libres dans le modèle, ce qui réduit sa complexité. Bien que la qualité de l’ajustement soit presque toujours améliorée par l’ajout de paramètres, l’ajustement excessif augmente la sensibilité du modèle aux changements des données d’entrée et peut ruiner sa capacité prédictive.
La raison principale de l’utilisation de l’AIC est de guider la sélection d’un modèle. Dans la pratique, elle est calculée pour un ensemble de modèles candidats et un ensemble de données donné. Le modèle ayant la plus petite valeur AIC est sélectionné comme le modèle de l’ensemble qui représente le mieux le « vrai » modèle, ou le modèle qui minimise la perte d’information, ce que l’AIC est conçu pour estimer.
Une fois que le modèle avec l’AIC minimum a été déterminé, une vraisemblance relative peut également être calculée pour chacun des autres modèles candidats afin de mesurer la probabilité de réduire la perte d’information par rapport au modèle avec l’AIC minimum. La vraisemblance relative peut aider l’enquêteur à décider si plus d’un modèle de la série doit être conservé pour un examen plus approfondi.
Le calcul de l’AIC est basé sur la formule générale suivante obtenue par Akaike1
![]()
où ![]() est le nombre de paramètres libres dans le modèle et
est le nombre de paramètres libres dans le modèle et ![]() est la valeur maximisée de la fonction de vraisemblance pour le modèle estimé.
est la valeur maximisée de la fonction de vraisemblance pour le modèle estimé.
Lorsque la taille de l’échantillon des données ![]() est faible par rapport au nombre de paramètres
est faible par rapport au nombre de paramètres![]() (certains auteurs disent que
(certains auteurs disent que ![]() n’est pas plus de quelques fois plus grand que
n’est pas plus de quelques fois plus grand que ![]() ), l’AIC ne sera pas aussi efficace pour protéger contre l’ajustement excessif. Dans ce cas, il existe une version corrigée de l’AIC donnée par :
), l’AIC ne sera pas aussi efficace pour protéger contre l’ajustement excessif. Dans ce cas, il existe une version corrigée de l’AIC donnée par :
![]()
On constate que l’AICc impose une pénalité plus importante que l’AIC lorsqu’il y a des paramètres supplémentaires. La plupart des auteurs semblent s’accorder sur le fait que l’AICc devrait être utilisé à la place de l’AIC dans toutes les situations.
Fonctions d’ajustement des probabilités – 24 nouvelles fonctions d’ajustement des probabilités ont été ajoutées à la bibliothèque d’ajustement standard.jfl. Ces fonctions, ainsi que certaines équations et formes graphiques, sont présentées ci-dessous :

Par exemple, le fichier d’ajustement de la fonction de densité lognormale contient l’équation de la densité lognormale lognormden(x,a,b), les équations pour l’estimation automatique des paramètres initiaux et les sept nouvelles fonctions de pondération.
[Variables]
x = col(1)
y = col(2)
réciproque_y = 1/abs(y)
reciprocal_ysquare = 1/y^2
réciproque_x = 1/abs(x)
réciproque_xsquare = 1/x^2
reciprocal_pred = 1/abs(f)
reciprocal_predsqr = 1/f^2
poids_Cauchy = 1/(1+4*(y-f)^2)
Fonctions d’estimation automatique des paramètres initiaux
trap(q,r)=.5*total(({0,q}+{q,0})[data(2,size(q))]*diff(r)[data(2,size(r))])
s=sort(complex(x,y),x)
u = sous-bloc(s,1,1,1, taille(x))
v = sous-bloc(s,2,1,2, size(y))
meanest = trap(u*v,u)
varest=trap((u-meanest)^2*v,u)
p = 1+varest/meanest^2
[Parameters]
a= if(meanest > 0, ln(meanest/sqrt(p)), 0)
b= if(p >= 1, sqrt(ln(p)), 1)
[Equation]
f=lognormden(x,a,b)
adapter f à y
« ajuster f à y avec le poids reciprocal_y
« Ajuster f à y avec un poids réciproque (reciprocal_ysquare)
« ajuster f à y avec le poids reciprocal_x
« Ajuster f à y avec le poids reciprocal_xsquare » « Ajuster f à y avec le poids reciprocal_xsquare
« ajuster f à y avec le poids reciprocal_pred
« ajuster f à y avec le poids reciprocal_predsqr
« ajuster f à y avec le poids weight_Cauchy
[Constraints]
b>0
[Options]
tolérance=1e-010
stepsize=1
itérations=200
Fonctions de poids dans la régression non linéaire – SigmaPlot Les éléments d’équation utilisent parfois une variable de poids dans le but d’assigner un poids à chaque observation (ou réponse) dans un ensemble de données de régression. Le poids d’une observation mesure son incertitude par rapport à la distribution de probabilités à partir de laquelle elle est échantillonnée. Un poids plus élevé indique une observation qui s’écarte peu de la moyenne réelle de sa distribution, tandis qu’un poids plus faible se réfère à une observation qui est davantage échantillonnée à partir de la queue de sa distribution.
Selon les hypothèses statistiques pour l’estimation des paramètres d’un modèle d’ajustement à l’aide de l’approche des moindres carrés, les poids sont, jusqu’à un facteur d’échelle, égaux à la réciproque des variances de population des distributions (gaussiennes) à partir desquelles les observations sont échantillonnées. Nous définissons ici un résidu, parfois appelé résidu brut, comme la différence entre une observation et la valeur prédite (la valeur du modèle d’ajustement) pour une valeur donnée de la (des) variable(s) indépendante(s). Si les variances des observations ne sont pas toutes identiques(hétéroscédasticité), une variable de pondération est nécessaire et le problème des moindres carrés pondérés, qui consiste à minimiser la somme pondérée des carrés des résidus, est résolu pour trouver les paramètres les mieux adaptés.
Notre nouvelle fonctionnalité permettra à l’utilisateur de définir une variable de poids en fonction des paramètres contenus dans le modèle d’ajustement. Sept fonctions de pondération prédéfinies ont été ajoutées à chaque fonction d’ajustement (les fonctions 3D sont légèrement différentes). Les sept exemples ci-dessous sont 1/y, 1/y2, 1/x, 1/x2, 1/prédit, 1/prédit2 et Cauchy.

Cette pondération adaptative plus générale s’applique notamment aux situations où les variances des observations ne peuvent être déterminées avant l’ajustement. Par exemple, si toutes les observations sont distribuées selon une distribution de Poisson, les moyennes de la population, qui sont ce que les valeurs prédites estiment, sont égales aux variances de la population. Bien que l’approche des moindres carrés pour l’estimation des paramètres soit conçue pour des données normalement distribuées, d’autres distributions sont parfois utilisées avec les moindres carrés lorsque d’autres méthodes ne sont pas disponibles. Dans le cas de données de Poisson, nous devons définir la variable de poids comme la réciproque des valeurs prédites. Cette procédure est parfois appelée « pondération par les valeurs prédites ».
Une autre application de la pondération adaptative consiste à obtenir des procédures robustes d’estimation des paramètres qui atténuent les effets des valeurs aberrantes. Il peut arriver que quelques observations d’un ensemble de données soient échantillonnées à partir de la queue de leur distribution avec une faible probabilité, ou que quelques observations soient échantillonnées à partir de distributions qui s’écartent légèrement de l’hypothèse de normalité utilisée dans l’estimation par les moindres carrés et contaminent ainsi l’ensemble de données. Ces observations aberrantes, appelées valeurs aberrantes de la variable réponse, peuvent avoir un impact significatif sur les résultats de l’ajustement car elles présentent des résidus (bruts ou pondérés) relativement importants et gonflent donc la somme des carrés que l’on cherche à minimiser.
Une façon d’atténuer les effets des valeurs aberrantes est d’utiliser une variable de poids qui est une fonction des résidus (et donc aussi une fonction des paramètres), où le poids attribué à une observation est inversement lié à la taille du résidu. La définition de la fonction de pondération à utiliser dépend d’hypothèses sur les distributions des observations (en supposant qu’elles ne soient pas normales) et d’un schéma permettant de décider de la taille du résidu à tolérer. La fonction de pondération de Cauchy est définie en termes de résidus, y-f où y est la valeur de la variable dépendante et f la fonction d’ajustement, et peut être utilisée pour minimiser l’effet des valeurs aberrantes.
poids_Cauchy = 1/(1+4*(y-f)^2)
L’algorithme d’estimation des paramètres que nous utilisons pour la pondération adaptative, les moindres carrés repondérés de manière itérative (IRLS), est basé sur la résolution d’une séquence de problèmes de moindres carrés à pondération constante où chaque sous-problème est résolu en utilisant notre implémentation actuelle de l’algorithme de Levenberg-Marquardt. Ce processus commence par l’évaluation des poids à l’aide des valeurs initiales des paramètres, puis par la minimisation de la somme des carrés à l’aide de ces poids fixes. Les paramètres les mieux adaptés sont ensuite utilisés pour réévaluer les poids.
Avec les nouvelles valeurs de poids, le processus ci-dessus de minimisation de la somme des carrés est répété. Nous continuons ainsi jusqu’à ce que la convergence soit atteinte. Le critère utilisé pour la convergence est que l’erreur relative entre la racine carrée de la somme des résidus pondérés pour les valeurs actuelles des paramètres et la racine carrée de la somme des résidus pondérés pour les valeurs des paramètres de l’itération précédente est inférieure à la valeur de tolérance fixée dans l’équation. Comme pour les autres procédures d’estimation, la convergence n’est pas garantie.
