sigmaplot-product-features

INPIXON

SigmaPlot Caractéristiques du produit

Nouvelles fonctionnalités et améliorations de SigmaPlot

Parcelles forestières
Graphiques de densité du noyau
10 nouvelles gammes de couleurs
Graphique de densité de points avec barres de moyenne et d’erreur standard
Légende Améliorations
- Formes de légende horizontales, verticales et rectangulaires
  - Curseur sur le côté ou sur la poignée supérieure ou inférieure
- - permet des légendes à plusieurs colonnes
- Interface utilisateur permettant de définir le nombre de colonnes de l’élément de légende dans la boîte de dialogue Propriétés. Les numéros de colonne autorisés sont affichés dans la liste déroulante
- Modifier le nombre de colonnes de l’élément de légende en sélectionnant et en faisant glisser la poignée du milieu dans la boîte de délimitation.
- Réorganiser les éléments de la légende
  - Dans la boîte de dialogue des propriétés – déplacer un ou plusieurs éléments de la légende vers le haut ou vers le bas à l’aide du contrôle haut/bas situé en haut de la zone de liste.
  - Par le déplacement du curseur – déplacer un ou plusieurs éléments de la légende vers le haut ou vers le bas. Sélectionnez le(s) élément(s) de la légende et utilisez les touches fléchées haut et bas du clavier pour vous déplacer à l’intérieur de la boîte de délimitation.
  - Sélection à l’aide de la souris et déplacement du curseur pour les éléments situés dans la boîte englobante
- Paramètres des propriétés des éléments de légende individuels – sélectionnez des éléments de légende individuels et utilisez la mini-barre d’outils pour modifier les propriétés.
  - Contrôle de la région vide de la boîte de légende à l’aide du curseur
  - Curseur sur la poignée d’angle
  - permet un redimensionnement proportionnel
- Ajouter un étiquetage direct simple
  - Prise en charge de l’étiquetage direct dans la boîte de dialogue des propriétés à l’aide de la case à cocher « Étiquetage direct ».
  - Dégrouper les éléments de la légende – les éléments individuels de la légende peuvent être déplacés vers des emplacements préférés et se déplacer en même temps que le graphique.
- La prise en charge du titre de la légende a été ajoutée (pas de titre par défaut). L’utilisateur peut ajouter un titre à la boîte de légende à l’aide du panneau des propriétés de la légende
- Inverser les éléments de la légende à l’aide du menu contextuel du clic droit
- Ouvrez les propriétés de la légende en double-cliquant sur Légende solide ou Légende texte.
- L’option Réinitialiser a été ajoutée aux légendes pour réinitialiser les options de légende par défaut.

Nouvelles fonctions d'analyse

Analyse en composantes principales (ACP)
Analyse de la covariance (ANCOVA)
Ajout de valeurs P aux comparaisons multiples pour les ANOVA non paramétriques
Suppression des choix de la boîte combo pour les niveaux de signification des comparaisons multiples et liaison du niveau de signification des comparaisons multiples au test principal (omnibus).
Ajout du critère d’information d’Akaike aux rapports de l’assistant de régression et de l’assistant d’ajustement dynamique, ainsi qu’à la boîte de dialogue Options des rapports.
Ajout du bouton Rerun dans le groupe SigmaStat
Mise à jour de la bibliothèque fit standard.jfl
- Ajout de fonctions de probabilité, au nombre de 24, pour l’ajustement de courbes ou la visualisation de fonctions.
- La valeur de tolérance pour toutes les équations a été modifiée pour utiliser la « e-notation » au lieu de la décimale fixe. Cela permet à l’utilisateur de lire la valeur sans avoir à la faire défiler.
- Ajouter sept fonctions de pondération à toutes les équations d’ajustement de courbe dans standard.jfl. Une légère variante a été ajoutée pour les équations 3D.

Nouvelles fonctionnalités de l'interface utilisateur

Réorganiser les éléments du carnet de notes dans une section en les faisant glisser
Nouveau fichier PDF du tutoriel SigmaPlot
Largeur des lignes à partir d’une colonne de la feuille de calcul

Nouvelles fonctions d'importation/exportation

Ajout des formats de fichiers SVG et SWF pour l’exportation de graphiques vectoriels évolutifs.
Ajout d’une exportation PDF vectorielle pour améliorer l’exportation PDF matricielle existante.
La prise en charge de l’importation et de l’exportation de fichiers a été ajoutée pour les versions 13 et 14 de Minitab, la version 9 de SAS, la version 19 de SPSS et la version 13 de Symphony.

SigmaPlot Caractéristiques du produit

Parcelle forestière

Le diagramme forestier est une forme de "méta-analyse" utilisée pour combiner plusieurs analyses portant sur la même question. La méta-analyse combine statistiquement les échantillons de chaque étude pour créer une statistique globale plus précise que l'ampleur de l'effet dans les études individuelles. Les valeurs individuelles de l'étude et leurs intervalles de confiance à 95 % sont représentés par des symboles carrés avec des barres d'erreur horizontales et la statistique globale de synthèse par un losange dont la largeur est égale à son intervalle de confiance à 95 %.

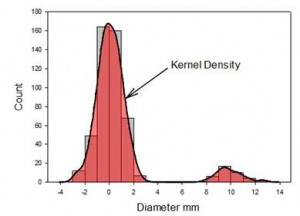
Densité du noyau

La caractéristique de densité du noyau génère une estimation de la distribution des données sous-jacentes. Ce résultat doit être comparé à l'histogramme en escalier. Il présente des avantages (pas de barres) et des inconvénients (perte d'informations sur le comptage) par rapport à l'histogramme et doit être utilisé conjointement avec ce dernier. Ils peuvent être créés simultanément.

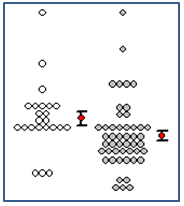
Densité de points avec barres de moyenne et d'erreur standard

Le calcul de la moyenne et de la barre d'erreur standard, symbole et barres d'erreur, a été ajouté au graphique de densité de points. Cela permet d'améliorer les autres statistiques possibles de l'affichage de la densité de points - moyenne, médiane, percentiles et diagramme en boîte.

Nouveaux schémas de couleurs

Dix nouvelles combinaisons de couleurs ont été mises en place. Trois exemples sont présentés ci-dessous :

Améliorations de la légende - Formes

Des formes de légende verticales, horizontales et rectangulaires sont désormais disponibles.

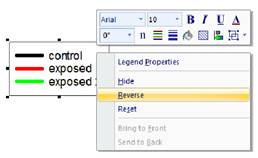
Ordre inverse de la légende

Vous pouvez maintenant choisir d'inverser l'ordre des éléments de la légende. Cela permet d'obtenir un ordre plus logique pour certains types de graphiques.

Réorganiser les éléments de la légende

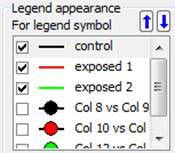
Il existe trois façons de réorganiser les éléments de la légende. Comme illustré ici, vous pouvez déplacer un ou plusieurs éléments de légende vers le haut ou vers le bas à l'aide des flèches haut/bas du panneau Légendes des Propriétés du graphique. Encore plus simple, il suffit de sélectionner l'élément dans la légende et d'utiliser les touches de déplacement vers le haut et vers le bas du clavier. Vous pouvez également sélectionner l'élément de légende et le faire glisser vers la nouvelle position à l'aide du curseur de la souris.

Edition des éléments de la légende dans la mini-barre d'outils

Les éléments de la légende peuvent désormais être modifiés en cliquant sur l'élément et en utilisant la mini-barre d'outils.

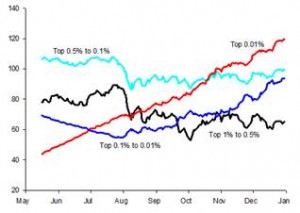
Étiquetage direct

La légende peut maintenant être dégroupée et les éléments individuels de la légende peuvent être placés à côté des parcelles appropriées. Les étiquettes se déplacent avec le graphique pour maintenir leur position par rapport au graphique. L'étiquette étant adjacente à la placette, l'identification visuelle de chaque placette est désormais beaucoup plus aisée.

Analyse en composantes principales (ACP)

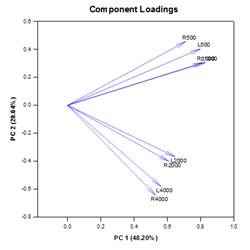
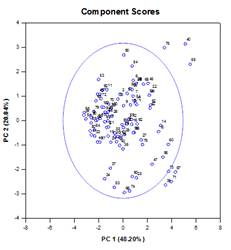
L'analyse en composantes principales (ACP) est une technique qui permet de réduire la complexité des données à haute dimension en les approximant avec moins de dimensions. Chaque nouvelle dimension est appelée composante principale et représente une combinaison linéaire des variables originales. La première composante principale tient compte de la plus grande variation possible des données. Chaque composante principale suivante rend compte de la plus grande partie possible de la variation restante et est orthogonale à toutes les composantes principales précédentes.

Vous pouvez examiner les composantes principales pour comprendre les sources de variation de vos données. Vous pouvez également les utiliser pour élaborer des modèles prédictifs. Si la plupart des variations de vos données existent dans un sous-ensemble à faible dimension, vous pouvez peut-être modéliser votre variable de réponse en termes de composantes principales. Vous pouvez utiliser les composantes principales pour réduire le nombre de variables dans la régression, le regroupement et d'autres techniques statistiques.

La sortie graphique consiste en des diagrammes de Scree, de saturation des composantes et de scores des composantes.

Analyse de la covariance (ANCOVA)

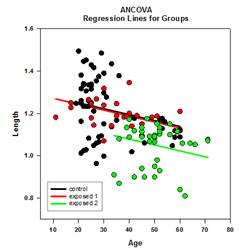
Un modèle d'ANOVA à un seul facteur est basé sur un plan complètement aléatoire dans lequel les sujets d'une étude sont échantillonnés au hasard dans une population et chaque sujet est ensuite assigné au hasard à l'un de plusieurs niveaux de facteurs ou traitements de sorte que chaque sujet a une probabilité égale de recevoir un traitement. Une hypothèse courante de ce modèle est que les sujets sont homogènes. Cela signifie que toute autre variable, pour laquelle il existe des différences entre les sujets, ne modifie pas de manière significative l'effet du traitement et ne doit pas être incluse dans le modèle. Cependant, il y a souvent des variables, hors du contrôle de l'enquêteur, qui affectent les observations au sein d'un ou de plusieurs groupes de facteurs, ce qui conduit à des ajustements nécessaires des moyennes de groupe, de leurs erreurs, des sources de variabilité et des valeurs P de l'effet de groupe, y compris les comparaisons multiples.

Ces variables sont appelées covariables. Il s'agit généralement de variables continues, mais elles peuvent également être catégoriques. Étant donné qu'ils sont généralement d'une importance secondaire pour l'étude et, comme mentionné ci-dessus, non contrôlables par l'enquêteur, ils ne représentent pas des facteurs d'effets principaux supplémentaires, mais peuvent néanmoins être inclus dans le modèle afin d'améliorer la précision des résultats. Les covariables sont également appelées variables de nuisance ou variables concomitantes.

ANCOVA (Analysis of Covariance) est une extension de l'ANOVA obtenue en spécifiant une ou plusieurs covariables comme variables supplémentaires dans le modèle. Si vous organisez les données ANCOVA dans une feuille de calcul SigmaPlot en utilisant le format de données indexées, une colonne représentera le facteur et une colonne représentera la variable dépendante (les observations) comme dans un plan ANOVA. En outre, vous aurez une colonne pour chaque covariable. L'utilisation d'un modèle incluant les effets des covariables permet d'expliquer davantage la variabilité de la valeur de la variable dépendante.

Cela réduit généralement la variance inexpliquée attribuée à la variabilité aléatoire de l'échantillonnage, ce qui augmente la sensibilité de l'ANCOVA par rapport au même modèle sans covariables (modèle ANOVA). Une sensibilité de test plus élevée signifie que des différences moyennes plus faibles entre les traitements deviendront significatives par rapport à un modèle ANOVA standard, augmentant ainsi la puissance statistique.

Pour illustrer l'utilisation de l'ANCOVA, prenons l'exemple d'une expérience au cours de laquelle les élèves sont assignés de manière aléatoire à l'un des trois types de méthodes d'enseignement et dont les résultats sont mesurés. L'objectif est de mesurer l'effet des différentes méthodes et de déterminer si l'une d'entre elles permet d'obtenir un score moyen significativement plus élevé que les autres. Les méthodes sont le cours magistral, l'auto-apprentissage et l'apprentissage coopératif. L'exécution d'une ANOVA à une voie sur ces données hypothétiques donne les résultats du tableau ci-dessous, sous l'en-tête de la colonne ANOVA. Nous concluons qu'il n'y a pas de différence significative entre les méthodes d'enseignement. Il convient également de noter que la variance inexpliquée par le modèle ANOVA, qui est due à la variabilité de l'échantillonnage aléatoire dans les observations, est estimée à 35,17.

Il est possible que les étudiants de notre étude bénéficient davantage d'une méthode que des autres, en fonction de leurs résultats scolaires antérieurs. Supposons que nous affinions l'étude pour inclure une covariable qui mesure une capacité antérieure, telle qu'une évaluation basée sur les normes (SBA) sanctionnée par l'État. En effectuant une ANCOVA à une voie sur ces données, on obtient les résultats figurant dans le tableau ci-dessous, sous l'intitulé de la colonne ANCOVA.

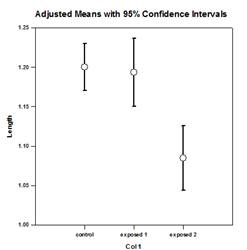
La moyenne ajustée indiquée dans le tableau pour chaque méthode est une correction de la moyenne du groupe pour contrôler les effets de la covariable. Les résultats montrent que les moyennes ajustées sont significativement différentes, la méthode Lecture étant la plus performante. Remarquez que les erreurs standard des moyennes ont diminué d'un facteur de presque trois, tandis que la variance due à la variabilité aléatoire de l'échantillon a diminué d'un facteur de dix. Une réduction de l'erreur est la conséquence habituelle de l'introduction de covariables et de la réalisation d'une analyse ANCOVA.

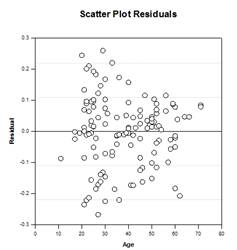
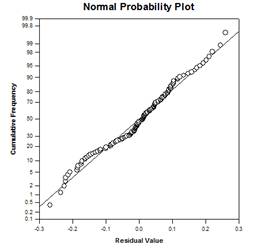
Il existe quatre graphiques de résultats d'ANCOVA - lignes de régression dans les groupes, diagramme de dispersion des résidus, moyennes ajustées avec intervalles de confiance et diagramme de probabilité de normalité :

Valeurs P pour les ANOVA non paramétriques

Les tests ANOVA non paramétriques dans SigmaPlot sont le test de Kruskal-Wallis (ANOVA à une voie sur les rangs) et le test de Friedman (ANOVA à une voie sur les rangs à mesures répétées). Tous deux proposent quatre procédures de test post-hoc pour déterminer la source des effets significatifs dans le facteur de traitement. Les quatre procédures sont Tukey, SNK, Dunn et Dunnett.

Les trois premières procédures peuvent être utilisées pour tester la signification de chaque comparaison par paire des groupes de traitement, tandis que les deux dernières peuvent être utilisées pour tester la signification des comparaisons par rapport à un groupe de contrôle. La méthode de Dunn est la seule procédure disponible si les groupes de traitement ont des tailles d'échantillon inégales.

Lorsqu'une procédure de test post-hoc est utilisée, le rapport contient un tableau reprenant les résultats des comparaisons par paire des niveaux de traitement. La dernière colonne du tableau indique si la différence de classement est significative ou non. Dans les versions précédentes de SigmaPlot, il n'y a pas de valeur p ajustée qui peut être comparée au niveau de signification de l'ANOVA (habituellement .05) pour déterminer la signification.

En effet, SigmaPlot déterminait la signification en comparant la statistique de test observée, calculée pour chaque comparaison, à une valeur critique de la distribution de la statistique obtenue à partir d'une table de recherche. SigmaPlot disposait de deux séries de tables de recherche pour les distributions de probabilités correspondant aux quatre méthodes post hoc, l'une pour un niveau de signification de 0,05 et l'autre pour un niveau de signification de 0,01.

Cette méthode a été récemment modifiée pour utiliser des procédures analytiques afin de calculer les valeurs p de ces distributions, ce qui a rendu les tables de recherche obsolètes. En raison de ce changement, nous sommes désormais en mesure de présenter les valeurs p ajustées pour chaque comparaison par paire. Cette modification permet également de supprimer la restriction consistant à utiliser 0,05 et 0,01 comme seuls niveaux de signification pour les comparaisons multiples. L'utilisateur peut donc saisir n'importe quel niveau de signification de la valeur P entre 0 et 1.

Critère d'information d'Akaike (AICc)

Le critère d'information d'Akaike (AIC) est une méthode permettant de mesurer la performance relative de l'ajustement d'un modèle de régression à un ensemble de données donné. Fondé sur le concept d'entropie de l'information, le critère offre une mesure relative de l'information perdue lors de l'utilisation d'un modèle pour décrire les données. Plus précisément, il s'agit d'un compromis entre la maximisation de la vraisemblance du modèle estimé (ce qui revient à minimiser la somme des carrés résiduels si les données sont normalement distribuées) et le maintien au minimum du nombre de paramètres libres dans le modèle, ce qui réduit sa complexité. Bien que la qualité de l'ajustement soit presque toujours améliorée par l'ajout de paramètres, l'ajustement excessif augmente la sensibilité du modèle aux changements des données d'entrée et peut ruiner sa capacité prédictive.

La raison principale de l'utilisation de l'AIC est de guider la sélection d'un modèle. Dans la pratique, elle est calculée pour un ensemble de modèles candidats et un ensemble de données donné. Le modèle ayant la plus petite valeur AIC est sélectionné comme le modèle de l'ensemble qui représente le mieux le "vrai" modèle, ou le modèle qui minimise la perte d'information, ce que l'AIC est conçu pour estimer. Une fois que le modèle avec l'AIC minimum a été déterminé, une vraisemblance relative peut également être calculée pour chacun des autres modèles candidats afin de mesurer la probabilité de réduire la perte d'information par rapport au modèle avec l'AIC minimum. La vraisemblance relative peut aider l'enquêteur à décider si plus d'un modèle de la série doit être conservé pour un examen plus approfondi.

Le calcul de l'AIC est basé sur la formule générale suivante obtenue par Akaike

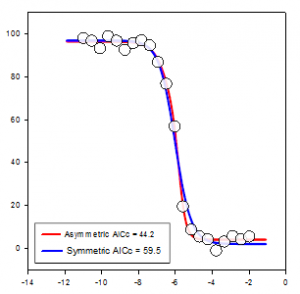
oùest le nombre de paramètres estimables dans le problème de régression, qui comprend les paramètres du modèle et la variance inconnue des observations, et est la valeur maximisée de la fonction de vraisemblance pour le modèle estimé.

Lorsque la taille de l’échantillon des données est faible par rapport au nombre de paramètres (certains auteurs disent que n’est pas plus de quelques fois plus grand que), l’AIC n’est pas aussi efficace pour protéger contre l’ajustement excessif. Dans ce cas, il existe une version corrigée de l’AIC donnée par

On constate que l'AICc impose une pénalité plus importante que l'AIC lorsqu'il y a des paramètres supplémentaires. La plupart des auteurs semblent s'accorder sur le fait que l'AICc devrait être utilisé à la place de l'AIC dans toutes les situations et c'est l'AICc qui est implémenté dans SigmaPlot. L'équation asymétrique du graphique est nettement meilleure que l'équation symétrique puisque sa valeur AICc est inférieure de plus de 7 unités à celle de l'équation symétrique - une règle empirique pour l'AICc. Si la différence est supérieure à 2, l'équation ayant la plus petite valeur AICc ne doit pas être considérée comme la meilleure, mais plutôt comme un candidat à la meilleure équation.

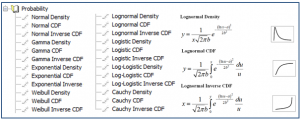
Fonctions de probabilité de régression non linéaire

24 nouvelles fonctions d'ajustement des probabilités ont été ajoutées à la bibliothèque d'ajustement standard.jfl. Ces fonctions, ainsi que certaines équations et formes graphiques, sont présentées ci-dessous.

Fonctions de pondération de la régression non linéaire

Il existe maintenant sept fonctions de pondération différentes intégrées dans chaque équation de régression non linéaire (les 3D sont légèrement différentes). Ces fonctions sont les suivantes : y réciproque, y réciproque au carré, x réciproque, x réciproque au carré, prédictions réciproques, prédictions réciproques au carré et Cauchy. L'algorithme des moindres carrés repondérés de manière itérative est utilisé pour permettre aux poids de changer au cours de chaque itération de régression non linéaire. Ainsi, la "pondération par les prédictions", une méthode couramment utilisée, peut être obtenue en sélectionnant l'option de pondération reciprocal_pred.

De même, la pondération de Cauchy (sélectionnez weight_Cauchy) peut être utilisée pour ajuster une équation à des données contenant des valeurs aberrantes et l'effet des valeurs aberrantes sera minimisé. Les utilisateurs peuvent créer leurs propres méthodes de pondération en termes de résidus et/ou de paramètres pour mettre en œuvre d'autres méthodes d'ajustement robustes. La section d'équation d'un fichier d'ajustement est présentée avec les sept fonctions de pondération intégrées.

Fonctionnalités de l'interface utilisateur - Réorganisez les éléments de votre carnet en les faisant glisser.

Les objets d'une section de carnet ne sont pas nécessairement créés dans un ordre logique. Vous pouvez désormais faire glisser les éléments d'une section vers de nouvelles positions afin de les placer de manière plus logique.

Un tutoriel SigmaPlot mis à jour

Le nouveau didacticiel facilite la création de graphiques pour la première fois. Il commence par des exemples simples et se complexifie progressivement.

Spécifier la largeur des lignes de tracé à partir d'une colonne de la feuille de calcul

Les valeurs de largeur de ligne peuvent désormais être saisies dans une colonne de la feuille de calcul. Ces valeurs peuvent être utilisées dans un graphique ou dans plusieurs graphiques de la page.

Nouveaux formats de fichiers d'exportation vectorielle

Les formats de fichiers SVG (Scalable Vector Graphics), SWF (Adobe Flash Player) et Vector PDF ont été ajoutés. Il s'agit de formats évolutifs dans lesquels aucune résolution n'est perdue lorsque l'on zoome à différents niveaux. SVG est le format graphique standard pour le web et SWF peut être utilisé avec Adobe Flash Player. Le format PDF étant très utilisé, le format PDF vectoriel est désormais associé au bouton Créer un PDF du ruban Accueil.

Mise à jour des formats des dossiers de candidature

La prise en charge de l'importation et de l'exportation de fichiers a été mise à jour pour les versions 13 et 14 de Minitab, la version 9 de SAS et la version 19 de SPSS.