シグマプロット製品の特徴

インピクソン

シグマプロット製品の特徴

SigmaPlotの新機能と改良点

森林圃場
カーネル密度プロット
10の新しい配色
ドット密度グラフ（平均値と標準誤差バー付き
レジェンドの改善
- 水平、垂直、長方形の凡例図形
  - カーソルをサイドまたは上下のハンドルに合わせる
- - 複数列の凡例が可能
- プロパティダイアログで凡例項目の列数を設定するユーザーインターフェイス。許容される列番号はコンボリストに表示される。
- バウンディング・ボックスの真ん中のハンドルを選択しドラッグして、凡例項目の列数を変更する。
- 凡例項目の並び替え
  - プロパティダイアログを通して – リストボックスの上部にある上下コントロールを使用して、1つまたは複数の凡例項目を上下に移動する。
  - カーソルの移動により、1つまたは複数の凡例項目を上下に移動する。凡例項目を選択し、キーボードの上下矢印キーでバウンディングボックス内を移動する。
  - バウンディング・ボックス内のアイテムをマウスで選択し、カーソルを動かす。
- 個々の凡例項目のプロパティ設定 – 個々の凡例項目を選択し、ミニツールバーを使用してプロパティを変更する。
  - カーソルでレジェンドボックスの空白領域をコントロール
  - カーソルをコーナーハンドルに合わせる
  - プロポーショナル・リサイズが可能
- シンプルなダイレクト・ラベルの追加
  - プロパティ・ダイアログで、”ダイレクト・ラベリング “チェックボックス・コントロールを使用して、”ダイレクト・ラベリング “をサポートする。
  - 凡例アイテムのグループ解除 – 個々の凡例アイテムを好きな場所に移動し、グラフと連動して移動することができます。
- 凡例タイトルのサポートが追加されました（デフォルトではタイトルなし）。ユーザーは、凡例プロパティパネルを使用して、凡例ボックスにタイトルを追加できます。
- 右クリックのコンテキストメニューを使用して、凡例項目を反転させる。
- 凡例ソリッドまたは凡例テキストのいずれかをダブルクリックして、凡例プロパティを開きます。
- 凡例にリセットが追加され、凡例オプションがデフォルトにリセットされます。

新しい分析機能

主成分分析（PCA）
共分散分析（ANCOVA）
ノンパラメトリックANOVAの多重比較にP値を追加
多重比較の有意水準に関するコンボボックスの選択肢を削除し、多重比較の有意水準をメイン（オムニバス）検定に結びつけた。
回帰ウィザードとダイナミックフィットウィザードのレポートとレポートオプションダイアログに赤池情報量規準を追加。
SigmaStatグループに再実行ボタンが追加されました。
フィット・ライブラリstandard.jflを更新
- 曲線フィッティングや関数の可視化のための確率関数を24個追加。
- すべての方程式の公差値が、固定10進数の代わりに「e-notation」を使用するように変更されました。これにより、ユーザーはスクロールせずに値を読むことができる。
- standard.jflのすべてのカーブフィット方程式に7つの重み付け関数を追加する。 3D方程式のために若干のバリエーションが追加されている。

新しいユーザーインターフェース機能

ノートブックの項目をドラッグして並べ替える
新しいSigmaPlotチュートリアルPDFファイル
ワークシートの列からの線幅

新しいインポート/エクスポート機能

スケーラブルなベクターグラフィックスのエクスポート用にSVGとSWFファイル形式を追加
既存のラスターPDFを改善するため、ベクターPDFエクスポートを追加。
Minitabのバージョン13と14、SASのバージョン9、SPSSのバージョン19、Symphonyのバージョン13のファイルのインポートとエクスポートがサポートされました。

シグマプロット製品の特徴

フォレスト・プロット

フォレストプロットは「メタ分析」の一形態で、同じ問題を扱う複数の分析を組み合わせるために用いられる。メタアナリシスは、寄与した各研究のサンプルを統計的に組み合わせ、個々の研究における効果量よりも正確な全体的な要約統計量を作成する。個々の研究値とその95％信頼区間は、水平のエラーバーを持つ四角いシンボルで示し、全体の要約統計量はその95％信頼区間と同じ幅を持つ菱形で示す。

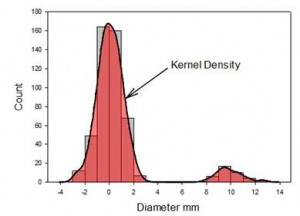
カーネル密度

カーネル密度機能は、基礎となるデータ分布の推定値を生成します。これはステップ状のヒストグラムと比較されるべきである。ヒストグラムよりも利点（バーがない）と欠点（カウント情報が失われる）があり、ヒストグラムと併用する必要がある。同時に作成することもできる。

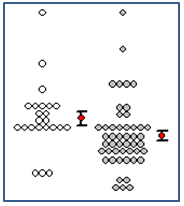
平均値と標準誤差のバー付きドット密度

ドット密度グラフに、平均＋標準エラーバー計算（シンボル＋エラーバー）が追加された。これにより、他のドット密度表示統計（平均値、中央値、パーセンタイル、箱ひげ図）が強化される。

新しい配色

10種類の新しいカラースキームが導入された。以下に3つの例を示す：

凡例の改善 - 形状

縦型、横型、長方形の凡例が利用できるようになった。

レジェンド逆順

凡例項目の順序を逆にすることを選択できるようになりました。これにより、グラフの種類によっては、より論理的な順序が得られる。

レジェンド・アイテムの再注文

凡例項目の並び替えには3つの方法がある。ここに示すように、グラフ・プロパティの「凡例」パネルにある上下矢印コントロールを使って、1つまたは複数の凡例項目を上下に動かすことができる。さらに簡単なのは、凡例で項目を選択し、キーボードの上下矢印キーを使うだけだ。または、凡例項目を選択し、マウスカーソルで新しい位置までドラッグする。

レジェンド項目のミニツールバー編集

凡例項目は、項目をクリックしてミニツールバーを使うことで編集できるようになった。

ダイレクト・ラベリング

凡例をグループから外し、個々の凡例項目を適切なプロットに隣接して配置できるようになった。ラベルはグラフと一緒に移動し、グラフに対する位置を維持する。ラベルがプロットに隣接しているため、各プロットの視覚的識別が非常に容易になった。

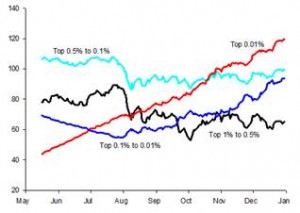
主成分分析（PCA）

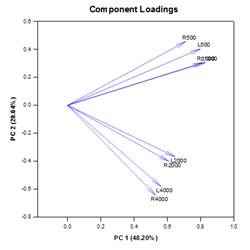
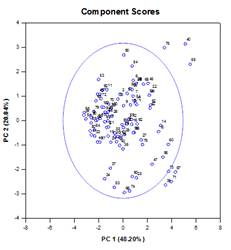
主成分分析（PCA）は、より少ない次元でデータを近似することにより、高次元データの複雑さを軽減する手法である。それぞれの新しい次元は主成分と呼ばれ、元の変数の線形結合を表す。第1主成分は、データのばらつきを可能な限り考慮する。後続の各主成分は、残りの変動のできるだけ多くを説明し、前のすべての主成分と直交する。

主成分を調べることで、データのばらつきの原因を理解することができます。また、予測モデルを作成する際にも使用できる。データの変動のほとんどが低次元の部分集合に存在する場合、主成分の観点から応答変数をモデル化できるかもしれません。主成分は、回帰、クラスタリング、その他の統計的手法において、変数の数を減らすために使用することができます。

グラフ出力は、Scree、Component Loadings、Component Scoresのプロットで構成されます。

共分散分析（ANCOVA）

単一因子ANOVA モデルは，研究の対象が母集団から無作為に抽出され，そして各対象が複数の因子水準または処置の1つに無作為に割り付けられ，各対象が等確率で処置を受ける完全無作為化デザインに基づく．このデザインに共通する仮定は、被験者は均質であるということである。これは、被験者間に差が存在する他の変数は、治療効果を有意に変化させないので、モデルに含める必要がないことを意味する。しかし、調査者がコントロールできない変数が、1つまたは複数の因子グループ内のオブザベーションに影響することがよくあり、グループ平均、その誤差、変動源、および多重比較を含むグループ効果のP値に必要な調整をもたらします。

これらの変数は共変量と呼ばれる。一般的には連続変数であるが、カテゴリー変数であることもある。これらは通常、研究にとって二次的な重要性を持ち、前述のように研究者がコントロールできないので、主効果因子を追加するものではないが、結果の精度を高めるためにモデルに含めることはできる。共変量は、厄介な変数や付随変数としても知られている。

ANCOVA (共分散分析)は，1つまたは複数の共変量をモデル中の追加変数として指定することによって得られるANOVAの拡張である．インデックス付きデータ形式を用いてANCOVAデータをSigmaPlotワークシートに配置すると、1列がANOVAデザインと同じように因子を表し、1列が従属変数（オブザベーション）を表します。さらに、共変量ごとに1つの列ができます。共変量の効果を含むモデルを使用する場合、従属変数の値にはより多くの説明される変動がある。

これは一般に，ランダム・サンプリング変動に起因する説明できない分散を減少させ，共変量なしの同じモデル（ANOVAモデル）と比較して，ANCOVAの感度を増加させる．より高い検定感度は，標準的なANOVA モデルと比較して，より小さな処理間の平均差が有意になることを意味し，それによって統計的検出力を増加させる．

ANCOVAの簡単な使用例として、生徒を3種類の教授法のいずれかに無作為に割り付け、その達成度を測定する実験を考えてみよう。目標は、さまざまな方法の効果を測定し、ある方法が他の方法よりも有意に高い平均スコアを達成するかどうかを判断することである。その方法は、講義、自習、協同学習である。この仮想データで一元配置分散分析を実行すると、下の表のANOVA列の見出しの下に結果が得られます。その結果、指導法に大きな違いは見られなかった。また，オブザベーションでの無作為抽出変動に起因するANOVAモデルによって説明されない分散は，35.17と推定されることに注意．

私たちの研究に参加した生徒が、それまでの学業成績に基づいて、他の方法よりもある方法からより多くの利益を得ている可能性はある。例えば、州公認のスタンダード・ベース・アセスメント（SBA）のような、事前の能力を測定する共変量を含むように研究を改良したとしよう。このデータに対してOne Way ANCOVAを実行すると、下の表のANCOVAの欄の見出しにあるような結果が得られる。

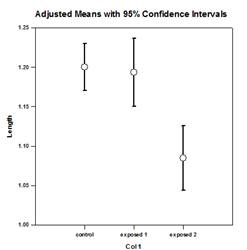
各方法の表に示されている修正平均は、共変量の影響をコントロールするために群平均を補正したものである。その結果、調整後の平均値には有意な差があり、レクチャー法がより成功したことが示された。平均値の標準誤差がほぼ3分の1に減少している一方で、無作為標本のばらつきによる分散が10分の1に減少していることに注目してください。誤差の減少は、共変量を導入してANCOVA分析を行うことの通常の結果である。

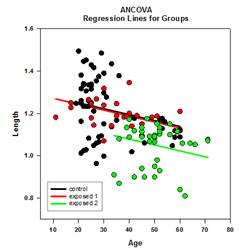
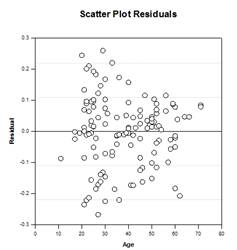
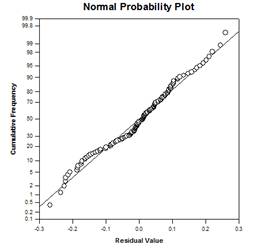
ANCOVAの結果グラフは4つある-群の回帰線，残差の散布図，信頼区間を伴う修正平均，および正規確率プロット．

ノンパラメトリックANOVAのP値

SigmaPlotでのノンパラメトリックANOVA検定は，Kruskal-Wallis検定 (順位に関する一元配置分散分析)およびFriedman検定 (順位に関する一元配置反復測定分散分析)です．これらはいずれも、治療因子における有意な効果の原因を決定するための4つの事後検定手順を提供する。 4つの手続きとは、Tukey、SNK、Dunn's、Dunnett'sである。

最初の3つの手続きは、治療群の各一対比較の有意性を検定するのに用いることができ、最後の2つは対照群との比較の有意性を検定するのに用いることができる。 Dunnの方法は、治療群の標本サイズが不均等である場合に利用できる唯一の方法である。

ポストホック検定の手順を使用する場合、治療レベルの一対比較の結果を一覧にした表が報告書に記載される。表の最後の列は、順位の差が有意か否かを示している。 SigmaPlotの以前のバージョンでは、有意性を決定するためにANOVAの有意水準(通常0.05)と比較できる修正p値が与えられていません。

これは、SigmaPlotが、各比較について計算された観測された検定統計量を、ルックアップテーブルから得られる統計量の分布の臨界値と比較することによって、有意性を決定していたからです。 SigmaPlotには、4つのポストホック法に対応する確率分布のルックアップテーブルが2セットあり、1セットは有意水準0.05のもの、もう1セットは有意水準0.01のものでした。

これは最近、これらの分布のp値を計算するために分析的手続きを使用するように変更され、ルックアップテーブルは廃止された。この変更により、各一対比較の修正p値を報告できるようになった。この変更により、多重比較のための唯一の有意水準として.05と.01を使用するという制約を取り除くことも可能になった。したがって、ユーザーは0から1までの任意の有効なP値の有意水準を入力することができる。

赤池情報量規準 (AICc)

赤池情報量規準（AIC）は、与えられたデータ集合に回帰モデルを適合させる際の相対的なパフォーマンスを測定する手法を提供する。情報エントロピーの概念に基づくこの基準は、データを記述するためにモデルを使用する際に失われる情報の相対的な尺度を提供する。より具体的には、推定モデルの尤度を最大化すること（データが正規分布している場合、残差平方和を最小化することと同じ）と、モデルの自由パラメータの数を最小に保ち、複雑さを軽減することのトレードオフを与える。適合度はパラメータを増やすことでほとんどの場合改善されるが、過剰適合は入力データの変化に対するモデルの感度を上げ、予測能力を台無しにする。

AICを使用する基本的な理由は、モデル選択の指針としてである。実際には、候補モデルの集合と与えられたデータセットに対して計算される。 AIC値が最小のモデルが、集合の中で「真の」モデルを最もよく表すモデル、つまりAICが推定するために設計された情報損失を最小化するモデルとして選択される。最小のAICを持つモデルが決定された後、最小のAICを持つモデルに対して情報損失を減らす確率を測定するために、他の候補モデルの各々について相対尤度を計算することもできる。相対尤度は、調査者がセット内の複数のモデルをさらに検討するために保持すべきかどうかを決定する際に役立ちます。

AICの計算は、Akaikeによって得られた以下の一般式に基づいている。

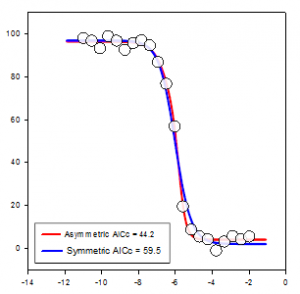
ここで，は回帰問題の推定可能なパラメータの数で，モデル・パラメータとオブザベーションの未知の分散を含む，は推定モデルの尤度関数の最大化された値である．

データのサンプルサイズが、パラメータの数に対して小さい場合（著者によっては、がの数倍以下である場合）、AICはオーバーフィッティングから保護するために、それほどうまく機能しません。この場合、AICの補正版は次式で与えられる。

余分なパラメータがある場合、AICcはAICよりも大きなペナルティを課すことがわかる。ほとんどの著者は、どのような状況でもAICの代わりにAICcを使うべきだということに同意しているようで、SigmaPlotに実装されているのはAICcです。グラフの非対称方程式は、AICc値が非対称方程式より7単位以上小さいので、非対称方程式の方が有意に優れている。もしその差が2より大きければ、AICc値がより小さい方程式を最良とみなすのではなく、最良の方程式の候補とみなすべきである。

非線形回帰確率関数

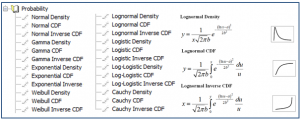
24の新しい確率フィット関数がフィットライブラリstandard.jflに追加されました。これらの関数と方程式、グラフの形を以下に示す。

非線形回帰重み付け関数

現在、各非線形回帰式には7つの異なる重み付け関数が組み込まれている（3Dは微妙に異なる）。これらの関数は、yの逆数、yの2乗の逆数、xの逆数、xの2乗の逆数、predictedsの逆数、predictedsの2乗の逆数、Caucyの逆数である。反復再重み付け最小2乗法は、各非線形回帰の反復中に重みを変更できるようにするために使用される。このように、reciprocal_pred重み付けオプションを選択することで、よく使われる方法である「予測値による重み付け」を得ることができる。

また、コーシー重み付け（weight_Cauchyを選択）を使用すると、外れ値を含むデータに方程式を当てはめることができ、外れ値の影響が最小化されます。ユーザは、他のロバスト・フィッティング手法を実装するために、残差および／またはパラメータに関して独自の重み付け方法を作成することができます。フィットファイルの方程式セクションは、7つの組み込み重み付け関数とともに表示されます。

ユーザーインターフェースの特徴 - ドラッグしてノートブックのアイテムを並べ替える

ノートブック・セクションのオブジェクトは、必ずしも論理的な順序で作成されるとは限りません。セクション内のアイテムを新しい位置にドラッグして、より論理的に配置できるようになりました。

シグマ・プロット・チュートリアルの更新

新しいチュートリアルでは、初めてグラフを作成する方でも簡単に作成できます。簡単な例から始まり、徐々に複雑になっていく。

ワークシートの列からプロットの線幅を指定する

線幅の値をワークシートの列に入力できるようになりました。これらの値は、グラフ内で使用することも、ページ上の複数のグラフにまたがって使用することもできる。

新しいベクター書き出しファイル形式

SVG（Scalable Vector Graphics）、SWF（Adobe Flash Player）、ベクターPDFファイル形式が追加されました。これらは、異なるレベルにズームしても解像度が失われないスケーラブルなフォーマットである。 SVGはウェブの標準グラフィック・フォーマットであり、SWFはAdobe Flash Playerで使用できる。 PDFの使用頻度が非常に高いため、ベクターPDFフォーマットがホームリボンのPDF作成ボタンに追加されました。

アプリケーション・ファイル形式の更新

ファイルのインポートおよびエクスポートのサポートが、Minitabのバージョン13および14、SASのバージョン9、SPSSのバージョン19に更新されました。