一般功能
新功能
2007 年,从第 11 版开始,SigmaStat 的功能和特性被整合到 SigmaPlot 中。 不过,2016 年 2 月 1 日,SigmaStat 4.0 发布,现在可作为独立产品使用。
以下是 SigmaStat 统计分析功能的多项改进:
- 主成分分析 (PCA) - 主成分分析是一种通过减少维度来降低高维数据复杂性的技术。
- 协方差分析(ANCOVA)--协方差分析是方差分析(ANOVA)的扩展,通过在模型中指定一个或多个协变量作为附加变量来实现。
- Cox 回归 - 包括分层比例危险模型,用于研究潜在风险因素对人群存活时间的影响。 输入数据可以是分类数据。
- 单样本 T 检验 - 检验群体均值等于指定值的假设。
- 几率比例检验和相对风险检验 - 这两种检验都是假设一种治疗方法对人群中某些特定事件的发生率没有影响。 几率比用于回顾性研究,以确定观察到事件发生后的治疗效果。 在前瞻性研究中,治疗组和对照组在事件发生前就已选定。
- Shapiro-Wilk 正态性检验 - 用于评估抽样数据的正态性,比 Kolmogorov-Smirnov 检验更准确。 用于许多统计检验的假设检查,也可直接用于工作表数据。
- 新结果图 - 方差分析剖面图:用于通过比较最小平方均值的平均值,分析多因素方差分析设计中各因素的主效应和高阶交互作用。
- 新概率变换 - SigmaStat 的变换语言新增了 34 个新函数,用于计算与许多研究领域中出现的分布相关的概率和分数。
- 新界面变化--非线性回归:易于使用的向导界面和更详细的报告。
- 新界面变化--快速变换:在工作表中执行计算的更简便方法。
- 新界面变化--新用户界面:允许用户更轻松地使用 Excel 工作表。
- Mann-Whitney 检验中添加的耶茨校正 - 耶茨连续性校正或耶茨卡方检验用于检验或然表的独立性,以评估两个观察样本是否来自同一分布。
- 改进的错误信息 - 改进的错误信息增加了方差分析假设检查失败时的信息。
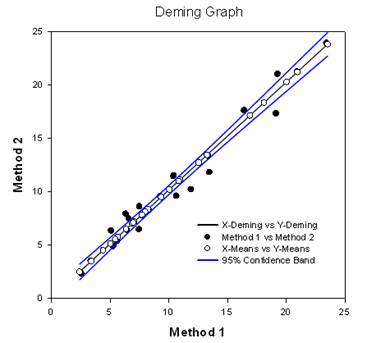
- 戴明回归 - 戴明回归允许 X 和 Y 变量出现误差 - 这是一种方法比较技术,其中 X 数据来自一种方法,Y 数据来自另一种方法。 戴明回归法基本上是将认为 X 值无误差的普通线性回归扩展到 X 和 Y(两种方法)都有误差的情况。 然后可以对假设进行检验,例如检验与 1.0 不同的斜率,以确定方法是否相同。 例如,它可用于比较两种测量相同物质的仪器,或比较两种检测图像中肿瘤的算法方法。 该图比较了这两种方法,以确定它们是不同还是相同。 报告提供统计结果。
- Akaike 信息准则 (AICc) - Akaike 信息准则现在可用于非线性回归报告。 这是一个拟合优度标准,也考虑了方程中的参数数量。 它也适用于非嵌套方程,例如在酶动力学分析中出现的非嵌套方程。
- 用于非线性回归的新概率函数 - 曲线拟合库中新增了 24 个概率函数。 为每个参数创建了自动初始参数估计方程。
- 非线性回归加权 - 现在每个非线性回归方程都内置了 7 种不同的加权函数(3D 稍有不同)。 这些函数是倒数 y、倒数 y 的平方、倒数 x、倒数 x 的平方、倒数 predicteds、倒数 predicteds 的平方和 Cauchy。 采用迭代重权最小二乘法算法,允许在每次非线性回归迭代过程中改变权重。
- 多重比较测试改进 - 有两项重要改进。 添加了非参数方差分析结果的 P 值。 这些都是以前不存在的。 此外,多重比较 P 值仅限于离散选择(0.05、0.01 等)。 这一限制已不复存在,可以使用任何有效的 P 值。
主要的新统计测试
主成分分析 (PCA) – 主成分分析是一种通过减少维度来降低高维数据复杂性的技术。 每个新维度称为一个主成分,代表原始变量的线性组合。 第一个主成分尽可能多地反映了数据的变化。 随后的每个主成分都尽可能多地考虑了剩余的变化,并与之前的所有主成分正交。
您可以通过检查主成分来了解数据的变化来源。 您还可以将它们用于形成预测模型。 如果数据中的大部分变化都存在于低维子集中,那么就可以用主成分对响应变量进行建模。 您可以使用主成分来减少回归、聚类和其他统计技术中的变量数量。 主成分分析法的主要目的是解释数据中的变异性来源,用较少的变量表示数据,同时保留大部分总变异。
主成分图示例
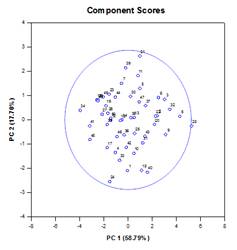
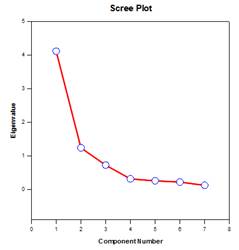
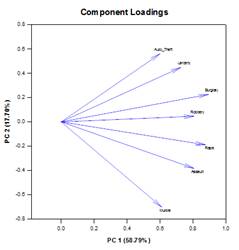
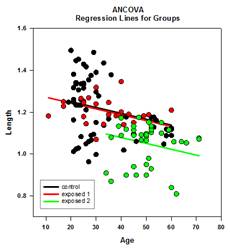
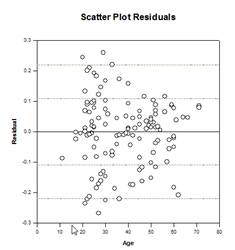
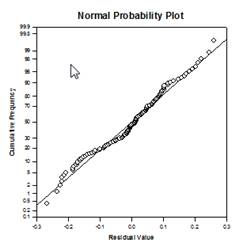
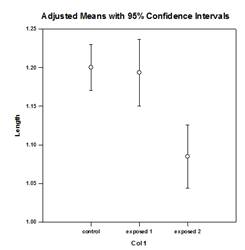
新的统计功能
多重比较 改进 – 对多重比较 P 值计算进行了重大改进。 下列多重比较程序、Tukey(非参数检验)、SNK(非参数检验)、Dunnett’s、Dunn’s(仅非 参数检验)和 Duncan 都不分析计算 p 值,而是使用特定分布的临界值查找表来确定计算出的检验 统计量是否代表组间均值的显著差异,必要时使用插值法。 因此,没有报告这些检验的 p 值,只报告了是否存在显著差异的结论。 这种方法的一个主要问题是,查找表只有两个显著性水平,即 0.05 和 0.01。 另一个问题是,许多客户想知道 p 值。 对于 SigmaPlot,已为所有事后检验程序编码了计算检验统计量分布的算法,从而使查找表不再适用。 因此,所有事后分析程序的调整后 p 值现在都放在报告中。 此外,不再需要将多重比较的显著性水平限制在 0.05 或 0.01。 相反,多重比较的显著性水平将与主(综合)检验的显著性水平相同。 这个 p 值没有限制,可以使用任何有效值。
阿卡克信息准则 (AICc)– 回归向导和动态拟合向导报告以及报告选项对话框中添加了阿卡克信息准则。 它提供了一种方法,用于衡量将回归模型拟合到给定数据集的相对性能。 该标准以信息熵的概念为基础,提供了使用模型描述数据时所损失信息的相对衡量标准。
更具体地说,它在最大化估计模型的可能性(与最小化残差平方和(如果数据呈正态分布)相同)和保持模型中自由参数数量最小、降低其复杂性之间进行了权衡。 虽然增加更多参数几乎总能提高拟合度,但过度拟合会增加模型对输入数据变化的敏感性,并可能破坏其预测能力。
使用 AIC 的基本原因是为了指导模型选择。 实际上,它是针对一组候选模型和给定的数据集计算出来的。 AIC 值最小的模型被选为模型集中最能代表 “真实 “模型的模型,或者说是信息损失最小的模型,而这正是 AIC 所要估算的。
在确定了 AIC 最小的模型后,还可以为其他每个候选模型计算相对可能性,以衡量相对于 AIC 最小的模型减少信息损失的概率。 相对可能性可以帮助研究人员决定是否应在模型集中保留多个模型供进一步考虑。
AIC 的计算基于Akaike1获得的以下一般公式
![]()
其中![]() 是模型中自由参数的个数,
是模型中自由参数的个数,![]() 是估计模型似然函数的最大值。
是估计模型似然函数的最大值。
当数据![]() 的样本量相对于参数
的样本量相对于参数![]() 的数量较少时(有些作者说当
的数量较少时(有些作者说当![]() 不超过
不超过![]() 的几倍时),AIC 就不能很好地防止过度拟合。 在这种情况下,AIC 的修正版为
的几倍时),AIC 就不能很好地防止过度拟合。 在这种情况下,AIC 的修正版为
![]()
可以看出,当有额外参数时,AICc 的惩罚比 AIC 更大。 大多数作者似乎都同意在所有情况下都应使用 AICc 而不是 AIC。
概率拟合函数– 在拟合库 standard.jfl 中添加了 24 个新的概率拟合函数。 这些函数以及一些等式和图形如下所示:

例如,对数正态密度函数的拟合文件包含对数正态密度方程 lognormden(x,a,b)、自动初始参数估计方程和七个新的加权函数。
[Variables]
x = col(1)
y = col(2)
reciprocal_y = 1/abs(y)
倒数平方 = 1/y^2
reciprocal_x = 1/abs(x)
x 平方倒数 = 1/x^2
reciprocal_pred = 1/abs(f)
reciprocal_predsqr = 1/f^2
权重_考奇 = 1/(1+4*(y-f)^2)
自动初始参数估计函数
trap(q,r)=.5*total(({0,q}+{q,0})[data(2,size(q))]*diff(r)[data(2,size(r))])
s=sort(complex(x,y),x)
u = subblock(s,1,1,1, size(x))
v = subblock(s,2,1,2, size(y))
meanest = trap(u*v,u)
varest=trap((u-meanest)^2*v,u)
p = 1+varest/meanest^2
[Parameters]
a= if(meanest> 0, ln(meanest/sqrt(p)), 0)
b= if(p>= 1, sqrt(ln(p)), 1)
[Equation]
f=lognormden(x,a,b)
拟合
“将 f 拟合为 y,权重为 reciprocal_y
“用权重倒易方拟合 f 到 y
“将 f 拟合为 y,权重为 reciprocal_x
“将 f 拟合为 y,权重为 reciprocal_xsquare
“将 f 拟合为 y,权重为 reciprocal_pred
“用权重 reciprocal_predsqr 将 f 拟合为 y
“用权重_考奇将 f 拟合到 y 上
[Constraints]
b>0
[Options]
容差=1e-010
stepize=1
迭代次数=200
非线性回归中的权重函数– SigmaPlot 方程项有时会使用权重变量,以便为回归数据集中的每个观测值(或响应)分配权重。 观测值的权重衡量的是观测值相对于取样概率分布的不确定性。 权重越大,表示观测值与其分布的真实平均值相差越小;权重越小,表示观测值与其分布的尾部取样越多。
根据使用最小二乘法估算拟合模型参数的统计假设,权重等于观测值取样的(高斯)分布的群体方差的倒数。 在此,我们将残差(有时也称为原始残差)定义为在给定自变量值下,观测值与预测值(拟合模型值)之间的差值。 如果观测值的方差不尽相同(异方差),则需要一个加权变量,并解决最小化残差加权平方和的加权最小二乘法问题,以找到最佳拟合参数。
我们的新功能将允许用户将权重变量定义为拟合模型所含参数的函数。 每个拟合函数都添加了七个预定义的权重函数(三维函数略有不同)。 下图中的七个分别是 1/y、1/y2、1/x、1/x2、1/predicted、1/predicteds2和 Cauchy。

在拟合之前无法确定观测值方差的情况下,可以应用这种更普遍的自适应加权。 例如,如果所有观测值都是泊松分布,那么预测值所估计的群体均值就等于群体方差。 虽然估计参数的最小二乘法是针对正态分布数据设计的,但在无法使用其他方法时,有时也会使用其他分布的最小二乘法。 对于泊松数据,我们需要将权重变量定义为预测值的倒数。 这一程序有时被称为 “预测值加权”。
自适应加权的另一个应用是获得稳健的参数估计程序,以减轻异常值的影响。 偶尔,数据集中可能会有几个观测值以很小的概率从其分布的尾部采样,或者有几个观测值的采样分布略微偏离最小二乘法估计中使用的正态性假设,从而污染了数据集。 这些异常观测值被称为响应变量中的异常值,会对拟合结果产生重大影响,因为它们具有相对较大的(原始或加权)残差,从而使最小化的平方和增大。
减轻异常值影响的一种方法是使用一个权重变量,它是残差的函数(因此也是参数的函数),其中分配给观测值的权重与残差的大小成反比。 使用何种加权函数的定义取决于对观测数据分布的假设(假设它们不是正态分布),以及决定可容忍残差大小的方案。 考奇加权函数是根据残差(y-f)定义的,其中 y 是因变量值,f 是拟合函数。
权重_考奇 = 1/(1+4*(y-f)^2)
我们用于自适应加权的参数估计算法–迭代再加权最小二乘法(IRLS),是基于求解一连串恒定加权最小二乘法问题,其中每个子问题都使用我们当前的Levenberg-Marquardt算法来求解。 这一过程首先使用初始参数值评估权重,然后利用这些固定权重最小化平方和。 然后使用最佳拟合参数重新评估权重。
利用新的权重值,重复上述最小化平方和的过程。 我们继续这样做,直到达到收敛为止。 收敛的标准是当前参数值的加权残差之和的平方根与上一次迭代参数值的加权残差之和的平方根之间的相对误差小于等式项中设定的容许误差值。 与其他估算程序一样,收敛性是无法保证的。
